Ας αποδείξουμε την τελευταία ισότητα (που αποδίδεται στον Hermite):
Αν
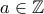 , τότε το ζητούμενο ισχύει. Έστω, λοιπόν, ότι
, τότε το ζητούμενο ισχύει. Έστω, λοιπόν, ότι  , οπότε
, οπότε  Τότε, υπάρχει
Τότε, υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε  και
και 
δηλαδή

Τότε, είναι:
![\displaystyle \left[ a \right] = \left[ {a + \frac{1}{m}} \right] = \cdots = \left[ {a + \frac{{k - 1}}{m}} \right] \displaystyle \left[ a \right] = \left[ {a + \frac{1}{m}} \right] = \cdots = \left[ {a + \frac{{k - 1}}{m}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/bb4a618bc16c6b0471382d03997b7e37.png)
και
![\displaystyle \left[ {a + \frac{k}{m}} \right] = \left[ {a + \frac{{k + 1}}{m}} \right] = \cdots = \left[ {a + \frac{{m - 1}}{m}} \right] = \left[ a \right] + 1, \displaystyle \left[ {a + \frac{k}{m}} \right] = \left[ {a + \frac{{k + 1}}{m}} \right] = \cdots = \left[ {a + \frac{{m - 1}}{m}} \right] = \left[ a \right] + 1,](/forum/ext/geomar/texintegr/latexrender/pictures/9118912a71d8f73737775ba570354e16.png)
οπότε
![\displaystyle \sum\limits_{j = 0}^{m - 1} {\left[ {a + \frac{j}{m}} \right]} = k\left[ a \right] + \left( {m - k} \right)\left( {\left[ a \right] + 1} \right) = m\left[ a \right] + m - k. \displaystyle \sum\limits_{j = 0}^{m - 1} {\left[ {a + \frac{j}{m}} \right]} = k\left[ a \right] + \left( {m - k} \right)\left( {\left[ a \right] + 1} \right) = m\left[ a \right] + m - k.](/forum/ext/geomar/texintegr/latexrender/pictures/8671755b2e84ff11135097d9175a3be5.png)
Εξάλλου, είναι
![\displaystyle m\left[ a \right] + m - k \le m\left[ a \right] + m\left\{ a \right\} = ma < m\left[ a \right] + m - k + 1, \displaystyle m\left[ a \right] + m - k \le m\left[ a \right] + m\left\{ a \right\} = ma < m\left[ a \right] + m - k + 1,](/forum/ext/geomar/texintegr/latexrender/pictures/39b14509559738765fb64a69ef14ec36.png)
οπότε
![\displaystyle \left[ {ma} \right] = m\left[ a \right] + m - k \displaystyle \left[ {ma} \right] = m\left[ a \right] + m - k](/forum/ext/geomar/texintegr/latexrender/pictures/dee1a5d71d4e5cfc1c24b436389d8fac.png)
και η απόδειξη ολοκληρώνεται.
Συντονιστές: achilleas, emouroukos, silouan
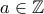 , τότε το ζητούμενο ισχύει. Έστω, λοιπόν, ότι
, τότε το ζητούμενο ισχύει. Έστω, λοιπόν, ότι  , οπότε
, οπότε  Τότε, υπάρχει
Τότε, υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε  και
και 

![\displaystyle \left[ a \right] = \left[ {a + \frac{1}{m}} \right] = \cdots = \left[ {a + \frac{{k - 1}}{m}} \right] \displaystyle \left[ a \right] = \left[ {a + \frac{1}{m}} \right] = \cdots = \left[ {a + \frac{{k - 1}}{m}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/bb4a618bc16c6b0471382d03997b7e37.png)
![\displaystyle \left[ {a + \frac{k}{m}} \right] = \left[ {a + \frac{{k + 1}}{m}} \right] = \cdots = \left[ {a + \frac{{m - 1}}{m}} \right] = \left[ a \right] + 1, \displaystyle \left[ {a + \frac{k}{m}} \right] = \left[ {a + \frac{{k + 1}}{m}} \right] = \cdots = \left[ {a + \frac{{m - 1}}{m}} \right] = \left[ a \right] + 1,](/forum/ext/geomar/texintegr/latexrender/pictures/9118912a71d8f73737775ba570354e16.png)
![\displaystyle \sum\limits_{j = 0}^{m - 1} {\left[ {a + \frac{j}{m}} \right]} = k\left[ a \right] + \left( {m - k} \right)\left( {\left[ a \right] + 1} \right) = m\left[ a \right] + m - k. \displaystyle \sum\limits_{j = 0}^{m - 1} {\left[ {a + \frac{j}{m}} \right]} = k\left[ a \right] + \left( {m - k} \right)\left( {\left[ a \right] + 1} \right) = m\left[ a \right] + m - k.](/forum/ext/geomar/texintegr/latexrender/pictures/8671755b2e84ff11135097d9175a3be5.png)
![\displaystyle m\left[ a \right] + m - k \le m\left[ a \right] + m\left\{ a \right\} = ma < m\left[ a \right] + m - k + 1, \displaystyle m\left[ a \right] + m - k \le m\left[ a \right] + m\left\{ a \right\} = ma < m\left[ a \right] + m - k + 1,](/forum/ext/geomar/texintegr/latexrender/pictures/39b14509559738765fb64a69ef14ec36.png)
![\displaystyle \left[ {ma} \right] = m\left[ a \right] + m - k \displaystyle \left[ {ma} \right] = m\left[ a \right] + m - k](/forum/ext/geomar/texintegr/latexrender/pictures/dee1a5d71d4e5cfc1c24b436389d8fac.png)
Η λύση που κυκλοφορεί για την τελευταία είναιMihalis_Lambrou έγραψε: ↑Κυρ Ιαν 07, 2018 1:07 pmΟι παρακάτω έχουν ξαναεμφανιστεί στο φορουμ αλλά τις αναρτώ χάριν πληρότητας.
Άσκηση 7. Δείξτε τις ταυτότητες
και γενικότερα
,

![f(x)={ \left [x \right ] + \left [x + \frac {1}{m} \right ] +...+ \left [x + \frac {m-1}{m} \right ]- \left [mx \right ] f(x)={ \left [x \right ] + \left [x + \frac {1}{m} \right ] +...+ \left [x + \frac {m-1}{m} \right ]- \left [mx \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/0aee07d1ae0e4e32052b862ee6d038bc.png)

 .
. είναι
είναι 
 ονομάζεται ταυτότητα Hermite.
ονομάζεται ταυτότητα Hermite. οφείλεται στον Matsuoka, "On a Proof of Hermite's Identity", The American Mathematical Monthly, τόμοςΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Ιαν 07, 2018 7:24 pm
Η λύση που κυκλοφορεί για την τελευταία είναι ...
 , έτος
, έτος  , σελίς
, σελίς  .
. ![\displaystyle{ \left [ \frac {[x]+m}{n } \right ] = \left [ \frac {x+m}{n } \right ] } \displaystyle{ \left [ \frac {[x]+m}{n } \right ] = \left [ \frac {x+m}{n } \right ] }](/forum/ext/geomar/texintegr/latexrender/pictures/08b9a8491fc51f0436e3f938d8ccee77.png) , για
, για 
![\displaystyle{ \left [ \frac {n}{3 } \right ]+ \left [ \frac {n+2}{6 } \right ] +\left [ \frac {n+4}{6 } \right ] = \left [ \frac {n}{2 } \right ] + \left [ \frac {n+3}{6} \right ] } \displaystyle{ \left [ \frac {n}{3 } \right ]+ \left [ \frac {n+2}{6 } \right ] +\left [ \frac {n+4}{6 } \right ] = \left [ \frac {n}{2 } \right ] + \left [ \frac {n+3}{6} \right ] }](/forum/ext/geomar/texintegr/latexrender/pictures/da9cc4611e2c5129747889f6fdb285dd.png)
Θέτουμε

![[2x]+[x+\frac{1}{3}]+[x+\frac{2}{3}]=[3x]+[x+\frac{1}{2}] [2x]+[x+\frac{1}{3}]+[x+\frac{2}{3}]=[3x]+[x+\frac{1}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/e70fbe178f8033e6e6dddf878e6ab4e0.png)

![[x]+[x+\frac{1}{2}]=[2x],[x]+[x+\frac{1}{3}]+[x+\frac{2}{3}]=[3x] [x]+[x+\frac{1}{2}]=[2x],[x]+[x+\frac{1}{3}]+[x+\frac{2}{3}]=[3x]](/forum/ext/geomar/texintegr/latexrender/pictures/dda7d24b2762a943b855f4cfa28408bd.png)
![[2x]+[x+\frac{1}{3}]+[x+\frac{2}{3}]=[x]+[x+\frac{1}{2}]+[x+\frac{1}{3}]+[x+\frac{2}{3}]=[3x]+[x+\frac{1}{2}]
[2x]+[x+\frac{1}{3}]+[x+\frac{2}{3}]=[x]+[x+\frac{1}{2}]+[x+\frac{1}{3}]+[x+\frac{2}{3}]=[3x]+[x+\frac{1}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/8aefb903d75acbba8620b8000a1c8d1c.png)
Θα αποδείξουμε αρχικά πως
![[x+m]=[x]+m [x+m]=[x]+m](/forum/ext/geomar/texintegr/latexrender/pictures/ebcd02c196dfa65dad7f7980988946fd.png) .
. ακέραιος με
ακέραιος με ![a=[x]+m a=[x]+m](/forum/ext/geomar/texintegr/latexrender/pictures/1b02bdf46746ef345fa68dff501cdcbc.png) . Έχουμε:
. Έχουμε:![[x+m]=[[x]+\{x\}+m]=[[x]+m+\{ x \}]=[a+\{ x \}]=a=[x]+m [x+m]=[[x]+\{x\}+m]=[[x]+m+\{ x \}]=[a+\{ x \}]=a=[x]+m](/forum/ext/geomar/texintegr/latexrender/pictures/30d011db76652678be2525b15326a9b4.png)
![\displaystyle{\left [\dfrac{[x]+m}{n} \right ]=\left [ \dfrac{x+m}{n} \right]\Leftrightarrow \left [ \dfrac{[x+m]}{n} \right ]=\left [\dfrac{x+m}{n} \right ]} \displaystyle{\left [\dfrac{[x]+m}{n} \right ]=\left [ \dfrac{x+m}{n} \right]\Leftrightarrow \left [ \dfrac{[x+m]}{n} \right ]=\left [\dfrac{x+m}{n} \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/473051db3d17c8857e9706375779ee57.png) .
. και αρκεί να αποδείξουμε πως:
και αρκεί να αποδείξουμε πως:![\displaystyle{\left [\dfrac{[y]}{n} \right ]=\left [\dfrac{y}{n} \right ]\Leftrightarrow \left [\dfrac{[y]}{n} \right ]=\left [\dfrac{[y]+\{y\}}{n} \right ]} \displaystyle{\left [\dfrac{[y]}{n} \right ]=\left [\dfrac{y}{n} \right ]\Leftrightarrow \left [\dfrac{[y]}{n} \right ]=\left [\dfrac{[y]+\{y\}}{n} \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/96d472a2fdad98889cef4abf64c97447.png) .
.![[y]\leq n-1 [y]\leq n-1](/forum/ext/geomar/texintegr/latexrender/pictures/1d91f379916830850b89b6a616bb9b8c.png) , τότε θα είναι
, τότε θα είναι ![\left [\dfrac{[y]}{n} \right ]=\left [\dfrac{[y]+\{y\}}{n} \right ]=0 \left [\dfrac{[y]}{n} \right ]=\left [\dfrac{[y]+\{y\}}{n} \right ]=0](/forum/ext/geomar/texintegr/latexrender/pictures/e3cc423d0304cc9b7abd2777c8e3a2d8.png) .
.![[y]\geq n [y]\geq n](/forum/ext/geomar/texintegr/latexrender/pictures/4dc3e2f0f6875c7ea35b9f12925d1569.png) .
.![[y]=nr+u [y]=nr+u](/forum/ext/geomar/texintegr/latexrender/pictures/233df46768a5ae7977f070bbe1e08fd4.png) , όπου
, όπου  .
.![\displaystyle{\left [r+\dfrac{u}{n} \right ]=\left [r+\dfrac{\{y\}+u}{n} \right ]} \displaystyle{\left [r+\dfrac{u}{n} \right ]=\left [r+\dfrac{\{y\}+u}{n} \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/4b5d1566f5eb39b5c6f017a2f0a2de3c.png)
 και
και  .
. και
και  .
.![\displaystyle{\left [r+\dfrac{u}{n} \right ]=\left [r+\dfrac{\{y\}+u}{n} \right ]=r} \displaystyle{\left [r+\dfrac{u}{n} \right ]=\left [r+\dfrac{\{y\}+u}{n} \right ]=r}](/forum/ext/geomar/texintegr/latexrender/pictures/ccfc5552856da0a825f4d97122c4002f.png) και το ζητούμενο έπεται.
και το ζητούμενο έπεται. που ικανοποιεί τα ακόλουθα κριτήρια:
που ικανοποιεί τα ακόλουθα κριτήρια: είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα.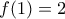
 .
. συμβολίζουμε τους θετικούς ακεραίους.
συμβολίζουμε τους θετικούς ακεραίους..nickthegreek έγραψε: ↑Σάβ Ιαν 13, 2018 4:33 pmΠρόβλημα 10Να αποδείξετε ότι υπάρχει συνάρτησηπου ικανοποιεί τα ακόλουθα κριτήρια:
a) Ηείναι γνησίως αύξουσα.
b)
c).
Μεσυμβολίζουμε τους θετικούς ακεραίους.
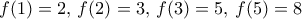 και λοιπά. Μυριζόμαστε Fibonacci
και λοιπά. Μυριζόμαστε Fibonacci όπου
όπου  .
.  τέτοια γραφή με
τέτοια γραφή με  τότε
τότε  (απλό με επαγωγή)
(απλό με επαγωγή)  μία τέτοια παράσταση του
μία τέτοια παράσταση του  , θέτουμε
, θέτουμε  και απλά ελέγχουμε τις δοθείσες συνθήκες.
και απλά ελέγχουμε τις δοθείσες συνθήκες. με παραστάσεις
με παραστάσεις  και
και  . Θέλουμε να δείξουμε ότι
. Θέλουμε να δείξουμε ότι  . Έστω ότι ίσχυε η ανάποδη ανισότητα. Χωρίς βλάβη
. Έστω ότι ίσχυε η ανάποδη ανισότητα. Χωρίς βλάβη  γιατί αλλιώς σβήνουμε τα ίσα
γιατί αλλιώς σβήνουμε τα ίσα  από τα δύο μέλη και συνεχίζουμε όπως παρακάτω. Θα είχαμε τότε
από τα δύο μέλη και συνεχίζουμε όπως παρακάτω. Θα είχαμε τότε οπότε
οπότε  , άρα
, άρα  και άρα
και άρα  αφού είναι άνισα. Τότε όμως
αφού είναι άνισα. Τότε όμως  , άτοπο. Αυτό δείχνει ότι η
, άτοπο. Αυτό δείχνει ότι η  είναι γνήσια αύξουσα.
είναι γνήσια αύξουσα. 

![\displaystyle{ \left [ \frac {[x]}{n } \right ] = \left [ \frac {x}{n } \right ] } \displaystyle{ \left [ \frac {[x]}{n } \right ] = \left [ \frac {x}{n } \right ] }](/forum/ext/geomar/texintegr/latexrender/pictures/0ddc62ace42d2cb0da3373865455481e.png) , όπου
, όπου  δοθείς.
δοθείς. τέτοιο ώστε
τέτοιο ώστε ![\displaystyle{ \left [ a [x] \right ] = \left [ a x \right ] \displaystyle{ \left [ a [x] \right ] = \left [ a x \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/bbf0dbed711dc00911fe16e38bd9dd43.png) για κάθε
για κάθε  , τότε το
, τότε το  είναι ίσο με το αντίστροφο κάποιου φυσικού.
είναι ίσο με το αντίστροφο κάποιου φυσικού. τέτοιο ώστε
τέτοιο ώστε ![\displaystyle{ \left [ a [x] \right ] = \left [ [a] x \right ] \displaystyle{ \left [ a [x] \right ] = \left [ [a] x \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/ba7b4f81b6fb275d931e774f8a63b2b4.png) για κάθε
για κάθε  , τότε
, τότε  .
. τέτοια ώστε
τέτοια ώστε ![\displaystyle{ \left [ a [bx] \right ] = \left [ [ab] x \right ] \displaystyle{ \left [ a [bx] \right ] = \left [ [ab] x \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/760601bf32d6351f3c44b398048c8384.png) για κάθε
για κάθε  , τότε τα
, τότε τα  και
και  είναι φυσικοί αριθμοί.
είναι φυσικοί αριθμοί.Εμπνευσμένη λύση. Την ίδια ιδέα μου είχε αναφέρει σε σχετική συζητήση ο Ραφαήλ Τσιάμης πριν καιρό. Η λύση που έχω εγώ είναι η εξής:Mihalis_Lambrou έγραψε: ↑Πέμ Ιαν 18, 2018 11:32 pm.nickthegreek έγραψε: ↑Σάβ Ιαν 13, 2018 4:33 pmΠρόβλημα 10Να αποδείξετε ότι υπάρχει συνάρτησηπου ικανοποιεί τα ακόλουθα κριτήρια:
a) Ηείναι γνησίως αύξουσα.
b)
c).
Μεσυμβολίζουμε τους θετικούς ακεραίους.
Για να κλείνει, δίνω λύση αλλά δεν χρησιμοποιώ ακέραιο μέρος.
Nίκο, έχεις λύση με ακέραιο μέρος;
Εξετάζοντας τις πρώτες μικρές τιμές θα διαπιστώσουμε ότικαι λοιπά. Μυριζόμαστε Fibonacci
όπου
.
Πραγματικά μας οδηγεί σε λύση χρησιμοποιώντας την ιδιότητα "κάθε φυσικός γράφεται κατά μοναδικό τρόπο ως άθροισμα μη διαδοχικών αριθμών Fibonacci" (πρόκειται για το θεώρημα Zeckendorf, που η απόδειξή του είναι απλή, με επαγωγή. Βλέπε για ιδιότητες και αποδείξεις εδώ). Θα χρησιμοποιήσω ακόμα ότι αντέτοια γραφή με
τότε
(απλό με επαγωγή)
Πίσω στην άσκηση.
Ανμία τέτοια παράσταση του
, θέτουμε
και απλά ελέγχουμε τις δοθείσες συνθήκες.
α) Έστωμε παραστάσεις
και
. Θέλουμε να δείξουμε ότι
. Έστω ότι ίσχυε η ανάποδη ανισότητα. Χωρίς βλάβη
γιατί αλλιώς σβήνουμε τα ίσα
από τα δύο μέλη και συνεχίζουμε όπως παρακάτω. Θα είχαμε τότε
οπότε
, άρα
και άρα
αφού είναι άνισα. Τότε όμως
, άτοπο. Αυτό δείχνει ότι η
είναι γνήσια αύξουσα.
β) Ισχύει εξ ορισμού.
γ)

 ικανοποιεί τις συνθήκες του προβλήματος. Με
ικανοποιεί τις συνθήκες του προβλήματος. Με  εννοώ τον χρυσό αριθμό. Η απόδειξη του ισχυρισμού αυτού δεν παρουσιάζει μεγάλες δυσκολίες αλλά είναι σχετικά επίπονη στο γράψιμο και την παραλείπω. Πιο δύσκολο είναι να βρεθει εξαρχής η εν λόγω συνάρτηση.
εννοώ τον χρυσό αριθμό. Η απόδειξη του ισχυρισμού αυτού δεν παρουσιάζει μεγάλες δυσκολίες αλλά είναι σχετικά επίπονη στο γράψιμο και την παραλείπω. Πιο δύσκολο είναι να βρεθει εξαρχής η εν λόγω συνάρτηση..nickthegreek έγραψε: ↑Τρί Ιαν 23, 2018 2:27 amHικανοποιεί τις συνθήκες του προβλήματος. Με
εννοώ τον χρυσό αριθμό. Η απόδειξη του ισχυρισμού αυτού δεν παρουσιάζει μεγάλες δυσκολίες αλλά είναι σχετικά επίπονη στο γράψιμο και την παραλείπω. Πιο δύσκολο είναι να βρεθει εξαρχής η εν λόγω συνάρτηση.
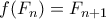 και το
και το  , έχουμε
, έχουμε  . Με άλλα λόγια
. Με άλλα λόγια  .
. είναι όλα τα λεφτά. Καταπληκτικό. Δεν θα το σκεφτόμουνα ποτέ! Ενθουσιάστηκα που το είδα.
είναι όλα τα λεφτά. Καταπληκτικό. Δεν θα το σκεφτόμουνα ποτέ! Ενθουσιάστηκα που το είδα.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες