 τέτοιες ώστε
τέτοιες ώστε 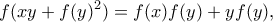 για κάθε
για κάθε 
Συντονιστές: achilleas, emouroukos, silouan
 τέτοιες ώστε
τέτοιες ώστε 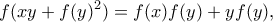 για κάθε
για κάθε 
Ωραία!
 η δοσμένη σχέση,
η δοσμένη σχέση,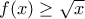 για
για 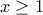
 με
με 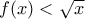 τότε
τότε 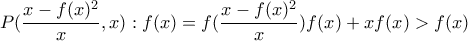 άτοπο.
άτοπο. .
. .
.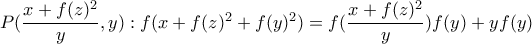
 και παίρνουμε
και παίρνουμε 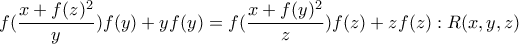 .
.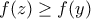 τότε
τότε 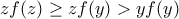 .
.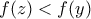 . Η εξίσωση
. Η εξίσωση 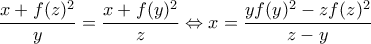
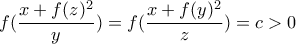 και η
και η 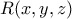 δίνει
δίνει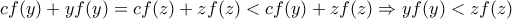 όπως ήθελα.
όπως ήθελα.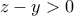 θα πρέπει
θα πρέπει 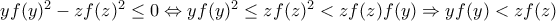 και τελειώσαμε.
και τελειώσαμε.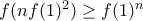 για κάθε φυσικό
για κάθε φυσικό  .
. ισχύει αφού
ισχύει αφού 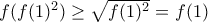
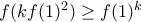 για κάποιο
για κάποιο  τότε
τότε 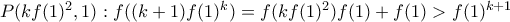 και επαγωγικά παίρνουμε το ζητούμενο.
και επαγωγικά παίρνουμε το ζητούμενο.
 . Έστω πως
. Έστω πως  .
. πάρε το
πάρε το  φυσικό με
φυσικό με 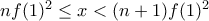 , οπότε
, οπότε 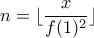 .
.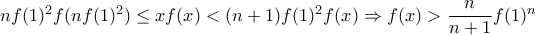 .
. αρκετά μεγάλο ώστε
αρκετά μεγάλο ώστε  οπότε
οπότε 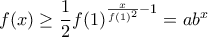 για κάποια
για κάποια 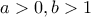 .
. και παίρνω μεγάλα
και παίρνω μεγάλα  (ώστε να ισχύει η προηγούμενη ανισότητα).
(ώστε να ισχύει η προηγούμενη ανισότητα).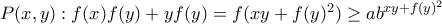 άρα
άρα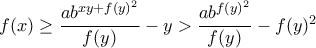
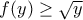 για μεγάλα
για μεγάλα  δίνει άτοπο λόγω του εκθετικού (δηλ το
δίνει άτοπο λόγω του εκθετικού (δηλ το 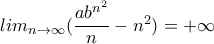 το οποίο είναι απλό).
το οποίο είναι απλό).
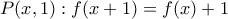
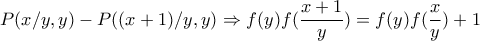
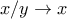 και παίρνω
και παίρνω 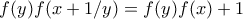 , για
, για  δίνει
δίνει 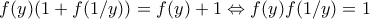
 ότι
ότι 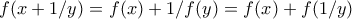 άρα
άρα  ,
, ικανοποιεί την Cauchy και αφού
ικανοποιεί την Cauchy και αφού  έπεται πως
έπεται πως 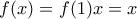 για κάθε
για κάθε  η οποία και επαληθεύει την αρχική.
η οποία και επαληθεύει την αρχική.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες