Διπλή ανισωση στους φυσικούς με παράμετρο

Al.Koutsouridis · #1

Να βρείτε όλες τις τιμές της παραμέτρου

, για τις οποίες το σύστημα των ανισώσεων

$\displaystyle{\dfrac{m}{n} < \sqrt{34} < \dfrac{m}{n} +\dfrac{a}{mn}}$

έχει άπειρες λύσεις στοτς φυσκούς αριθμούς m,n

.

Ορέστης Λιγνός · #2

Al.Koutsouridis έγραψε: ↑
Παρ Δεκ 02, 2022 4:22 pm
Να βρείτε όλες τις τιμές της παραμέτρου , για τις οποίες το σύστημα των ανισώσεων

$\displaystyle{\dfrac{m}{n} < \sqrt{34} < \dfrac{m}{n} +\dfrac{a}{mn}}$

έχει άπειρες λύσεις στους φυσικούς αριθμούς .

Αρχίζουμε με έναν Ισχυρισμό.

Ισχυρισμός: Για κάθε x,y

φυσικούς με 34x^2-y^2>0

, είναι $34x^2-y^2 \geq 9$ .
Απόδειξη: Έστω ότι 34x^2-y^2=k

, με $k \in \{1,2,3,4,5,6,7,8 \}$ . Δουλεύοντας $\pmod 17$ , απορρίπτουμε τις τιμές 3,5,6

και

. Για τις τιμές k=1

και

, αυτές απορρίπτονται από την Θεωρία των τύπου Pell εξισώσεων (δείτε π.χ. στον Nagel, σελ. 201-204). Για την τιμή k=4

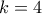τέλος, αυτή ανάγεται στην k=1

, καθώς αν

34x^2-y^2=4,

είναι $2 \mid y$ , άρα αν $y=2\ell$ , είναι $17x^2-2\ell^2=2,$ οπότε και το

είναι άρτιος, άρα αν x=2m

, προκύπτει τελικά

$34m^2-\ell^2=1,$

δηλαδή αναγόμαστε στην περίπτωση k=1

$\blacksquare$

Από τον Ισχυρισμό είναι,

$\sqrt{34}>\dfrac{m}{n} \Rightarrow 34n^2>m^2 \Rightarrow 34n^2 \geq m^2+9$ , οπότε προκύπτει ότι

$34-\dfrac{m^2}{n^2}=\dfrac{34n^2-m^2}{n^2} \geq \dfrac{9}{n^2}$ .

Τώρα, από την δεύτερη ανίσωση είναι

$34<(\dfrac{m}{n} +\dfrac{a}{mn})^2 \Rightarrow 34-\dfrac{m^2}{n^2}<\dfrac{a^2}{m^2n^2}+\dfrac{2a}{n^2},$

άρα προκύπτει ότι $\dfrac{a^2}{m^2n^2}+\dfrac{2a}{n^2} > \dfrac{9}{n^2} \Rightarrow a^2+2am^2>m^2 \Rightarrow a^2>(9-2a)m^2,$

οπότε αν $a <\dfrac{9}{2}$ τότε έχουμε ότι $m^2<\dfrac{a^2}{9-2a},$ δηλαδή το

μπορεί να πάρει πεπερασμένο αριθμό τιμών. Για κάθε τιμή m_0

του

όμως, είναι

$\sqrt{34} < \dfrac{m_0}{n} +\dfrac{a}{m_0n}} \Rightarrow n<\dfrac{m_0+\dfrac{a}{m_0}}{\sqrt{34}},$

δηλαδή και το

παίρνει πεπερασμένο αριθμό τιμών, άρα συνολικά δεν έχουμε άπειρες λύσεις (m,n)

, άτοπο.

Συνεπώς, πρέπει $a \geq \dfrac{9}{2}$ . Για να δούμε ότι όλα αυτά τα

επαληθεύουν, αρκεί προφανώς να επαληθεύσουμε τις ανισώσεις για $a=\dfrac{9}{2}$ . Από την Θεωρία των τύπου Pell εξισώσεων η εξίσωση

34n^2-m^2=9

έχει άπειρες λύσεις, και κάθε τέτοια λύση (m_0,n_0)

επαληθεύει τις ανισώσεις

$\dfrac{m_0}{n_0} <\sqrt{34}<\dfrac{m_0}{n_0}+\dfrac{9}{2m_0n_0},$

καθώς η μεν αριστερή είναι προφανής αφού 34n_0^2=m_0^2+9>m_0^2,

ενώ για την δεξιά μετά από ύψωση στο τετράγωνο αρκεί να δείξουμε ότι

$34<\dfrac{m_0^2}{n_0^2}+\dfrac{81}{4m_0^2n_0^2}+\dfrac{9}{n_0^2},$

που είναι προφανές αφού

$\dfrac{m_0^2}{n_0^2}+\dfrac{1}{4m_0^2n_0^2}+\dfrac{1}{n_0^2}>\dfrac{m_0^2}{n_0^2}+\dfrac{9}{n_0^2}=\dfrac{m_0^2+9}{n_0^2}=34$

Άρα, λύσεις είναι όλα τα $a \geq \dfrac{9}{2}$ .

Σημείωση: Γενικά, για την τύπου Pell εξίσωση x^2-dy^2=k

, αν αυτή έχει μία λύση (θεμελιώδης λύση) (x_0,y_0)

, τότε αν

η θεμελιώδης λύση της εξίσωσης x^2-dy^2=1

(που πάντα υπάρχει αν το

δεν είναι τέλειο τετράγωνο), τότε σύμφωνα με την ταυτότητα Brahmagupta

(u_0x_0 + dv_0y_0)^2 - d(v_0x_0 + u_0y_0)^2 = (u_0^2 - dv_0^2) (x_0^2 - dy_0^2) = k,

άρα από την λύση (x_0,y_0)

, βρίσκουμε την λύση (u_0x_0+dv_0y_0,v_0x_0+u_0y_0)

, οπότε συνεχίζοντας έτσι προκύπτουν άπειρες λύσεις στην εξίσωση x^2-dy^2=k

.

(Στην δική μας περίπτωση, η εξίσωση x^2-34y^2=-9

με

και

έχει τη θεμελιώδη λύση (5,1)

, ενώ η εξίσωση x^2-34y^2=1

έχει θεμελιώδη λύση την (35,6)

).

Al.Koutsouridis · #3

Εχει βγει σε χριστουγεννιάτικη παγανιά ο Ορέστης

. Για την ιστορία, το πρόβλημα είναι το υπαριθμόν 5287 του περιοδικού "Μαθηματικά Στο Σχολείο", τεύχος 9/10, 2012. Αν και εμφανισιακά, ίσως να μην είναι ελκυστική, θεώρησα ότι αξίζει τον κόπο.

Διπλή ανισωση στους φυσικούς με παράμετρο

Διπλή ανισωση στους φυσικούς με παράμετρο

Re: Διπλή ανισωση στους φυσικούς με παράμετρο

Re: Διπλή ανισωση στους φυσικούς με παράμετρο

Μέλη σε σύνδεση