 , για τους οποίους υπάρχουν πολυώνυμα μιας μεταβλητής
, για τους οποίους υπάρχουν πολυώνυμα μιας μεταβλητής  και
και  , τέτοια ώστε η ισότητα
, τέτοια ώστε η ισότητα 
να ισχύει για όλες τις τιμές του
 εκτός από πεπερασμένο αριθμό.
εκτός από πεπερασμένο αριθμό.Συντονιστές: achilleas, emouroukos, silouan
 , για τους οποίους υπάρχουν πολυώνυμα μιας μεταβλητής
, για τους οποίους υπάρχουν πολυώνυμα μιας μεταβλητής  και
και  , τέτοια ώστε η ισότητα
, τέτοια ώστε η ισότητα 
 εκτός από πεπερασμένο αριθμό.
εκτός από πεπερασμένο αριθμό. χαρακτηριστικής ίσης με το μηδέν.
χαρακτηριστικής ίσης με το μηδέν. 
 Παρατηρούμε ότι για
Παρατηρούμε ότι για  η ζητούμενη ισότητα είναι αδύνατη.
η ζητούμενη ισότητα είναι αδύνατη. Για
Για  όπου
όπου  δεν υπάρχουν τα πολυώνυμα
δεν υπάρχουν τα πολυώνυμα 
 Για
Για  όπου
όπου  τα πολυώνυμα υπάρχουν
τα πολυώνυμα υπάρχουν 
 όπου
όπου 
 με
με  ώστε να ισχύει η προτεινόμενη σχέση.
ώστε να ισχύει η προτεινόμενη σχέση.  δεν έχουν κοινό διαιρέτη (ο
δεν έχουν κοινό διαιρέτη (ο ![\mathbb{K}[X] \mathbb{K}[X]](/forum/ext/geomar/texintegr/latexrender/pictures/acff9afd043f94bc2d22685611f5ce26.png) είναι δακτύλιος μονοσήμαντης ανάλυσης), οπότε μεταξύ άλλων δεν έχουν κοινές ρίζες.
είναι δακτύλιος μονοσήμαντης ανάλυσης), οπότε μεταξύ άλλων δεν έχουν κοινές ρίζες.![\color{blue}[P(x)Q(x+d)-P(x+d)Q(x)]x(x+1)=Q(x)Q(x+d) \color{blue}[P(x)Q(x+d)-P(x+d)Q(x)]x(x+1)=Q(x)Q(x+d)](/forum/ext/geomar/texintegr/latexrender/pictures/470334d3ccd755f2d46c538c2756e47c.png)

 είναι ανάγωγο άρα και πρώτο στοιχείο στον δακτύλιο
είναι ανάγωγο άρα και πρώτο στοιχείο στον δακτύλιο ![\mathbb{K}[X] \mathbb{K}[X]](/forum/ext/geomar/texintegr/latexrender/pictures/acff9afd043f94bc2d22685611f5ce26.png) (επειδή ο
(επειδή ο ![\mathbb{K}[X] \mathbb{K}[X]](/forum/ext/geomar/texintegr/latexrender/pictures/acff9afd043f94bc2d22685611f5ce26.png) είναι δακτύλιος μονοσήμαντης ανάλυσης οι έννοιες ανάγωγο και πρώτο στοιχείο ταυτίζονται) και διαιρεί το δεύτερο μέλος της
είναι δακτύλιος μονοσήμαντης ανάλυσης οι έννοιες ανάγωγο και πρώτο στοιχείο ταυτίζονται) και διαιρεί το δεύτερο μέλος της  θα υπάρχουν δυο εκδοχές που αμφότερες οδηγούν σε άτοπο:
θα υπάρχουν δυο εκδοχές που αμφότερες οδηγούν σε άτοπο:

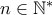 ορίζουμε
ορίζουμε 
 για κάθε
για κάθε 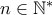
 Επειδή
Επειδή  γράφουμε
γράφουμε 
 και διαγράφοντας τον παράγοντα
και διαγράφοντας τον παράγοντα  κατά μέλη λαμβάνουμε
κατά μέλη λαμβάνουμε=(x+d)\tilde{Q}(x)\tilde{Q}(x+d) [P(x)(x+d)\tilde{Q}(x+d)-P(x+d)x\tilde{Q}(x)](x+1)=(x+d)\tilde{Q}(x)\tilde{Q}(x+d)](/forum/ext/geomar/texintegr/latexrender/pictures/c50257396dbdec37ab797ae6a9d838b6.png)
 η τελευταία γίνεται
η τελευταία γίνεται  οπότε επειδή
οπότε επειδή  θα πρέπει
θα πρέπει  και συνεπώς
και συνεπώς 

 Υποθέτουμε ότι το ζητούμενο ισχύει για
Υποθέτουμε ότι το ζητούμενο ισχύει για 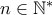


![[P(x)f_n(x+d)\tilde{Q}(x+d)-P(x+d)f_n(x)\tilde{Q}(x)]x(x+1) [P(x)f_n(x+d)\tilde{Q}(x+d)-P(x+d)f_n(x)\tilde{Q}(x)]x(x+1)](/forum/ext/geomar/texintegr/latexrender/pictures/c36e853a2c17f95d14237d6c25708983.png)

 είναι ρίζα του
είναι ρίζα του 
 έχουμε
έχουμε 
 βρίσκουμε
βρίσκουμε 


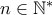 ορίζουμε
ορίζουμε 
 για κάθε
για κάθε 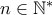
 Επειδή
Επειδή  γράφουμε
γράφουμε  οπότε για
οπότε για  ισχύει
ισχύει Υποθέτουμε ότι το ζητούμενο ισχύει για
Υποθέτουμε ότι το ζητούμενο ισχύει για 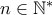 οπότε
οπότε 
![[P(x)h_n(x+d)\tilde{Q}(x+d)-P(x+d)h_n(x)\tilde{Q}(x)]x(x+1) [P(x)h_n(x+d)\tilde{Q}(x+d)-P(x+d)h_n(x)\tilde{Q}(x)]x(x+1)](/forum/ext/geomar/texintegr/latexrender/pictures/55039c08a93435d8f64846cc36c4fc09.png)

 στην τελευταία σχέση έχουμε
στην τελευταία σχέση έχουμε
 θα έχουμε
θα έχουμε 




 αρκεί να θεωρήσουμε
αρκεί να θεωρήσουμε  ,
, 
 αρκεί να θεωρήσουμε
αρκεί να θεωρήσουμε  ,
, 
 Για
Για  με
με  θεωρούμε
θεωρούμε 

 βρίσκούμε
βρίσκούμε (Σ)
(Σ) που να ικανοποιεί τη (Σ)
που να ικανοποιεί τη (Σ)

 το μοναδικό πολυώνυμο βαθμού το πολύ
το μοναδικό πολυώνυμο βαθμού το πολύ 
 (https://en.wikipedia.org/wiki/Polynomial_interpolation)
(https://en.wikipedia.org/wiki/Polynomial_interpolation) και
και 

 με
με 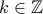 με
με 
 θα ικανοποιεί την πολυωνυμική ισότητα (Σ).
θα ικανοποιεί την πολυωνυμική ισότητα (Σ). Για
Για  με
με  και
και  θεωρούμε
θεωρούμε 

 βρίσκούμε
βρίσκούμε (Σ2)
(Σ2) που να ικανοποιεί τη (Σ2)
που να ικανοποιεί τη (Σ2)

 το μοναδικό πολυώνυμο βαθμού το πολύ
το μοναδικό πολυώνυμο βαθμού το πολύ 

 και
και 

 με
με 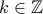 με
με 
 θα ικανοποιεί την πολυωνυμική ισότητα (Σ2).
θα ικανοποιεί την πολυωνυμική ισότητα (Σ2).
 , με
, με  αρνητικό ακέραιο μικρότερο ή ίσο του
αρνητικό ακέραιο μικρότερο ή ίσο του  ήταν λανθασμένη. Προστέθηκε η διορθωμένη εκδοχή της, ενώ η περίπτωση
ήταν λανθασμένη. Προστέθηκε η διορθωμένη εκδοχή της, ενώ η περίπτωση  , με
, με  θετικό ακέραιο μεγαλύτερο ή ίσο του
θετικό ακέραιο μεγαλύτερο ή ίσο του  έμεινε ως έχει (με τη διαφορά ότι το
έμεινε ως έχει (με τη διαφορά ότι το  απλοποιήθηκε σε
απλοποιήθηκε σε  )
)Ενδιαφέρον, δεδομένου ότι το 2006 σε τεστ επιλογής της Βουλγαρίας για την Διεθνή Μαθηματική Ολυμπιάδα τέθηκε το εξής θέμα:Al.Koutsouridis έγραψε: ↑Κυρ Μάιος 12, 2024 4:30 pmΘα ήθελα να ευχαριστήσω τον Ιάσωνα για την λύση και το χρόνο του. Για την ιστορία η άσκηση είναι από την ολυμπιάδα "Υψηλά πρότυπα" για το έτος 2021/22, του πανεπιστημίου Ανώτατη Σχολή Οικονομικών (Ρωσία).
![\displaystyle{P,Q\in \mathbb{R}[x]} \displaystyle{P,Q\in \mathbb{R}[x]}](/forum/ext/geomar/texintegr/latexrender/pictures/24a088fa9b4eb292599869f70660b394.png) , για τα οποία ισχύει
, για τα οποία ισχύει
 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης