Με βάση, λοιπόν, τις δύο προτάσεις, μπορεί να αποδειχθεί το αρχικό πρόβλημα.
Λύση του προβλήματος
(1):
Ο γεωμετρικός τόπος του σημείου

είναι η ευθεία συμμετρική του ύψους του τριγώνου

από το

ως προς την μεσοκάθετο του

.
Απόδειξη: Έστω

το αντιδιαμετρικό του

ως προς τον περιγεγραμμένο κύκλο του

.
Αφού

τότε

.
Άρα

σταθερό.
Έστω

το σημείο τομής των

. Από την πρόταση 2 το

θα κινείται σε ευθεία που θα διέρχεται από σημείο

ώστε το τετράπλευρο

να είναι παραλληλόγραμμο, δηλαδή το

θα είναι το ορθόκεντρο του τριγώνου

, αφού

και

.
Επιπλέον από γνωστό θεώρημα το σημείο

κινείται πάνω στο ύψος από το

του

όσο τα

βρίσκονται στο ίδιο ημιεπίπεδο με το

που ορίζει ο φορέας του

.
Συνεπώς ο γεωμετρικός τόπος του

είναι η ευθεία που περιέχει το

και το

.
Τέλος το σημείο

δεν είναι παρά το αντιδιαμετρικό του

ως προς τον κύκλο διερχόμενο από τα

, που με βάση την πρόταση 1 κινείται σε ευθεία κάθετη στο

, συγκεκριμένα στην συμμετρική ευθεία του γεωμετρικού τόπου του

, ως προς τον γεωμετρικό τόπο του περίκεντρου, δηλαδή της μεσοκαθέτου του

.
Λύση του προβλήματος
(2):
Ο γεωμετρικός τόπος του σημείου

είναι παραβολή που διέρχεται από τα

αν

και υπερβολή που διέρχεται από τα

σε κάθε άλλη περίπτωση.
Απόδειξη: Η σχέση

εξακολουθεί να ισχύει, άρα και το γεγονός ότι το

κινείται σε ευθεία διερχόμενη από το

.
Το σημείο

εξακολουθεί να είναι το αντιδιαμετρικό σημείο του

ως προς τον κύκλο διερχόμενο από τα

. Άρα από την πρόταση 1 το

κινείται σε υπερβολή, αν ο γεωμετρικός τόπος του

δεν είναι παράλληλος στο

. Η υπερβολή αυτή θα διέρχεται από τα

διότι

και

.
Τέλος από την πρόταση 2 έχουμε ότι ο γεωμετρικός τόπος του

θα είναι ευθεία παράλληλη στο

αν και μόνο αν

, όμως

.
Άρα

, που υποδηλώνει ότι τα τρίγωνα

είναι όμοια, και κατ' επέκταση ίσα, αφού έχουν το

κοινό. Με άλλα λόγια πρέπει να ισχύει

για να είναι από την πρόταση 1 ο γεωμετρικός τόπος του

παραβολή.
 και σημεία
και σημεία  πάνω στις κάθετες των
πάνω στις κάθετες των  που διέρχονται από τα
που διέρχονται από τα 
 και τα
και τα  βρίσκονται στο ίδιο ημιεπίπεδο που ορίζει η ευθεία από τα
βρίσκονται στο ίδιο ημιεπίπεδο που ορίζει η ευθεία από τα  .
.  το σημείο τομής των καθέτων των
το σημείο τομής των καθέτων των  που διέρχονται από τα
που διέρχονται από τα  αντίστοιχα.
αντίστοιχα.  καθώς μεταβάλλεται η γωνία
καθώς μεταβάλλεται η γωνία  .
. είναι εκατέρωθεν του ημιεπιπέδου που ορίζει η ευθεία από τα
είναι εκατέρωθεν του ημιεπιπέδου που ορίζει η ευθεία από τα  .
. .
. και ευθεία στην οποία κινείται ένα σημείο
και ευθεία στην οποία κινείται ένα σημείο  .
.
 ευθείες και ένα σταθερό σημείο σε καθεμία, έστω
ευθείες και ένα σταθερό σημείο σε καθεμία, έστω  και
και  . Αν τα
. Αν τα  κινούνται στις ευθείες από τα
κινούνται στις ευθείες από τα  αντίστοιχα έτσι ώστε
αντίστοιχα έτσι ώστε  να είναι σταθερό και τα
να είναι σταθερό και τα  των
των  κινείται σε ευθεία που διέρχεται από σταθερό σημείο ανεξάρτητα της τιμής του
κινείται σε ευθεία που διέρχεται από σταθερό σημείο ανεξάρτητα της τιμής του 
 των
των  αντίστοιχα.
αντίστοιχα. είναι σταθερά, και έχουμε ότι το τετράπλευρο
είναι σταθερά, και έχουμε ότι το τετράπλευρο  είναι τραπέζιο, με την ευθεία από τα
είναι τραπέζιο, με την ευθεία από τα  να είναι παράλληλη στις δύο παράλληλες του τραπεζίου και να διέρχεται από το κέντρο της
να είναι παράλληλη στις δύο παράλληλες του τραπεζίου και να διέρχεται από το κέντρο της 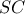 , οπότε προκύπτει ότι και το
, οπότε προκύπτει ότι και το  θα είναι μέσω του
θα είναι μέσω του  , άρα το σημείο
, άρα το σημείο  είναι σταθερό και ο ζητούμενος γεωμετρικός τόπος είναι η ευθεία που διέρχεται από το
είναι σταθερό και ο ζητούμενος γεωμετρικός τόπος είναι η ευθεία που διέρχεται από το  την ευθεία διερχόμενη από τα
την ευθεία διερχόμενη από τα  την ευθεία που διέρχεται από τα
την ευθεία που διέρχεται από τα  αντίστοιχα, με
αντίστοιχα, με  με
με  σταθερό αριθμό.
σταθερό αριθμό. αρκεί να βρεθεί το σημείο τομής της μεσοκαθέτου του
αρκεί να βρεθεί το σημείο τομής της μεσοκαθέτου του  .
. , για την οποία θα ισχύει
, για την οποία θα ισχύει  .
. , από την οποία μας ενδιαφέρει η κλίση για να βρεθεί και η κλίση της μεσοκάθετης, που θα είναι αντίθετη της αντίστροφης κλίσης του φορέα των
, από την οποία μας ενδιαφέρει η κλίση για να βρεθεί και η κλίση της μεσοκάθετης, που θα είναι αντίθετη της αντίστροφης κλίσης του φορέα των 
 θέτουμε
θέτουμε  και μετά από πράξεις έχουμε:
και μετά από πράξεις έχουμε: , που θα είναι η τεταγμένη του
, που θα είναι η τεταγμένη του  θα έχουμε
θα έχουμε  και
και  που μετά από πράξεις δίνει
που μετά από πράξεις δίνει  που είναι παραβολή.
που είναι παραβολή. .
. έχουμε
έχουμε  και
και  , που μετά από πράξεις και χρησιμοποιώντας το
, που μετά από πράξεις και χρησιμοποιώντας το  προκύπτει ότι
προκύπτει ότι  που είναι υπερβολή.
που είναι υπερβολή.
 τότε
τότε  (1)
(1) είναι
είναι  και η απόσταση των
και η απόσταση των 
 , επίσης έστω
, επίσης έστω  τα ίχνη του
τα ίχνη του  αντίστοιχα.
αντίστοιχα.

 σταθερό.
σταθερό. βρεθεί έξω από τα τμήματα
βρεθεί έξω από τα τμήματα  .
. στην περίπτωση που η ευθεία είναι παράλληλη στο
στην περίπτωση που η ευθεία είναι παράλληλη στο 

 τότε
τότε  .
. σταθερό.
σταθερό. το σημείο τομής των
το σημείο τομής των  . Από την πρόταση 2 το
. Από την πρόταση 2 το  να είναι παραλληλόγραμμο, δηλαδή το
να είναι παραλληλόγραμμο, δηλαδή το  και
και  .
. , που με βάση την πρόταση 1 κινείται σε ευθεία κάθετη στο
, που με βάση την πρόταση 1 κινείται σε ευθεία κάθετη στο  και υπερβολή που διέρχεται από τα
και υπερβολή που διέρχεται από τα  εξακολουθεί να ισχύει, άρα και το γεγονός ότι το
εξακολουθεί να ισχύει, άρα και το γεγονός ότι το  . Άρα από την πρόταση 1 το
. Άρα από την πρόταση 1 το  και
και  .
. , όμως
, όμως  .
. , που υποδηλώνει ότι τα τρίγωνα
, που υποδηλώνει ότι τα τρίγωνα  είναι όμοια, και κατ' επέκταση ίσα, αφού έχουν το
είναι όμοια, και κατ' επέκταση ίσα, αφού έχουν το  κοινό. Με άλλα λόγια πρέπει να ισχύει
κοινό. Με άλλα λόγια πρέπει να ισχύει