 του τριγώνου
του τριγώνου  εφάπτεται των πλευρών
εφάπτεται των πλευρών 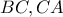 και
και  στα σημεία
στα σημεία  και
και  , αντίστοιχα. Αν
, αντίστοιχα. Αν  είναι το αντιδιαμετρικό σημείο του
είναι το αντιδιαμετρικό σημείο του  ( στον κύκλο
( στον κύκλο  ) και οι ευθείες
) και οι ευθείες  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  να δείξετε ότι οι ευθείες
να δείξετε ότι οι ευθείες  και
και  είναι παράλληλες.
είναι παράλληλες.Συντονιστές: vittasko, silouan, Doloros
 του τριγώνου
του τριγώνου  εφάπτεται των πλευρών
εφάπτεται των πλευρών 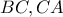 και
και  στα σημεία
στα σημεία  και
και  , αντίστοιχα. Αν
, αντίστοιχα. Αν  είναι το αντιδιαμετρικό σημείο του
είναι το αντιδιαμετρικό σημείο του  ( στον κύκλο
( στον κύκλο  ) και οι ευθείες
) και οι ευθείες  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  να δείξετε ότι οι ευθείες
να δείξετε ότι οι ευθείες  και
και  είναι παράλληλες.
είναι παράλληλες. η τομή των
η τομή των  και
και  .
. ανήκει στην πολική του
ανήκει στην πολική του  ως προς τον εγγεγραμμένο κύκλο.
ως προς τον εγγεγραμμένο κύκλο. ανήκει στην πολική του
ανήκει στην πολική του  ως προς τον εγγεγραμμένο κύκλο, δηλαδή στην
ως προς τον εγγεγραμμένο κύκλο, δηλαδή στην  , άρα και το
, άρα και το  ανήκει στην πολική του
ανήκει στην πολική του  ως προς τον εγγεγραμμένο κύκλο.
ως προς τον εγγεγραμμένο κύκλο. είναι η
είναι η  .
. .
. ταυτίζεται με την
ταυτίζεται με την  , δηλαδή με την
, δηλαδή με την  . Όμως
. Όμως  .
. .
. έχουμε πως
έχουμε πως  . Από το ισοσκελές
. Από το ισοσκελές  είναι
είναι  .
.  (1).
(1). , οπότε το
, οπότε το  είναι εγγράψιμο.
είναι εγγράψιμο. (2).
(2). .
.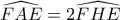 και
και  , οπότε το
, οπότε το  είναι το περίκεντρο του
είναι το περίκεντρο του 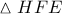 , οπότε
, οπότε  , και αφού επίσης
, και αφού επίσης  , έχουμε την ''αλυσίδα'' ισοτήτων :
, έχουμε την ''αλυσίδα'' ισοτήτων : .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης