
- συνευθειακότητα με το έγκεντρο.png (48.79 KiB) Προβλήθηκε 1500 φορές
Μια πρόοδο που έχω κάνει τις τελευταίες μέρες που νομίζω πως είναι ένα βήμα πριν τη λύση του προβλήματος:
Έστω

το μέσο του

και

το σημείο τομής των

και

.
Λόγω του ότι το

είναι μέσο της

, έχουμε πως

.
Αρκεί να αποδειχθεί πως η

είναι παράλληλη στη διχοτόμο της

.
Έστω πως η

και

τέμνουν τις

και

στα σημεία

και

αντίστοιχα.
Tο τετράπλευρο

είναι πλήρες και έτσι το δεύτερο σημείο τομής των περιγεγραμμένων κύκλων των τριγώνων

και
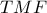
, έστω

, είναι το σημείο

του τετραπλεύρου.
Έστω πως το

ανήκει στη διχοτόμο της

. Αν

οι προβολές του

στις

και

αντίστοιχα, τότε θα ήταν

.
Όμως λόγω του ότι η ευθεία

είναι η ευθεία

του πλήρες τετραπλεύρου τετραπλεύρου, έχουμε πως η

είναι κάθετη στην ευθεία

του τετραπλεύρου, που είναι η
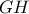
. Άρα αυτό θα αποδείκνυε πως η

είναι παράλληλη στη διχοτόμο της

και το ζητούμενο θα προέκυπτε.
Ξέρουμε ταυτόχρονα πως το σημείο

ανήκει στον περιγεγραμμένο κύκλο του τριγώνου

. Άρα αν πράγματι το

άνηκε στη διχοτόμο του

, τότε θα ήταν

.
Εκτελώντας νόμο ημιτόνων στα τρίγωνα

και

προκύπτει πως οι περιγεγραμμένοι κύκλοι των τριγώνων

και

πρέπει να είναι ίσοι και εκτελώντας πάλι νόμο ημιτόνων στα τρίγωνα

και
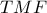
προκύπτει πως πρέπει

.
Αν αποδείξουμε δηλαδή πως

προκύπτει το ζητούμενο!!
Αν και προσπάθησα πολύ να αποδείξω την τελευταία ισότητα, δεν τα κατάφερα και κατέληξα σε περίπλοκες τριγωνομετρικές σχέσεις. Παρόλα αυτά πιστεύω πως η τελευταία ισότητα είναι πιο προσιτή από το αρχικό πρόβλημα.



 ,
,  το μέσον της
το μέσον της  και
και  τα σημεία επαφής των εγκύκλων
τα σημεία επαφής των εγκύκλων  με τις
με τις  αντίστοιχα.
αντίστοιχα. προς τις
προς τις  αντίστοιχα, τέμνονται στο
αντίστοιχα, τέμνονται στο  .
. το έγκεντρο του
το έγκεντρο του  , δείξτε οτι τα σημεία
, δείξτε οτι τα σημεία  είναι συνευθειακά.
είναι συνευθειακά.
 το μέσο του
το μέσο του  και
και  το σημείο τομής των
το σημείο τομής των  και
και  .
. .
. είναι παράλληλη στη διχοτόμο της
είναι παράλληλη στη διχοτόμο της  .
. και
και  τέμνουν τις
τέμνουν τις  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα.
αντίστοιχα. είναι πλήρες και έτσι το δεύτερο σημείο τομής των περιγεγραμμένων κύκλων των τριγώνων
είναι πλήρες και έτσι το δεύτερο σημείο τομής των περιγεγραμμένων κύκλων των τριγώνων  και
και 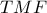 , έστω
, έστω  , είναι το σημείο
, είναι το σημείο  του τετραπλεύρου.
του τετραπλεύρου. οι προβολές του
οι προβολές του  .
.  του πλήρες τετραπλεύρου τετραπλεύρου, έχουμε πως η
του πλήρες τετραπλεύρου τετραπλεύρου, έχουμε πως η  του τετραπλεύρου, που είναι η
του τετραπλεύρου, που είναι η 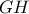 . Άρα αυτό θα αποδείκνυε πως η
. Άρα αυτό θα αποδείκνυε πως η  . Άρα αν πράγματι το
. Άρα αν πράγματι το  .
. και
και  προκύπτει πως οι περιγεγραμμένοι κύκλοι των τριγώνων
προκύπτει πως οι περιγεγραμμένοι κύκλοι των τριγώνων  .
.
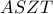 και ας είναι
και ας είναι  τα σημεία τομής των
τα σημεία τομής των  με την
με την  με κοινή διαγώνιο
με κοινή διαγώνιο  είναι παραλληλόγραμμο και συνεπώς
είναι παραλληλόγραμμο και συνεπώς 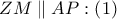
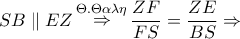

 η ημιπερίμετρος του τριγώνου
η ημιπερίμετρος του τριγώνου  και
και  η ημιπερίμετρος του τριγώνου
η ημιπερίμετρος του τριγώνου 
 ) τότε
) τότε 
 και
και 
 .
.


 και
και 

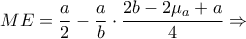
 .
.
 διχοτόμος της
διχοτόμος της 
 και
και  διχοτόμος της γωνίας
διχοτόμος της γωνίας  του εν λόγω παραλληλογράμμου (που ταυτίζεται με τη γωνία του τριγώνου
του εν λόγω παραλληλογράμμου (που ταυτίζεται με τη γωνία του τριγώνου  εφάπτονται εστω στο σημείο
εφάπτονται εστω στο σημείο  της
της  τέμνει τις
τέμνει τις  αντίστοιχα.
αντίστοιχα. αντίστοιχα.
αντίστοιχα.  , από το αντίστροφο γνωστής πρότασης, το
, από το αντίστροφο γνωστής πρότασης, το  .
.  είναι ισοσκελές εκ κατασκευής και συνεπώς η
είναι ισοσκελές εκ κατασκευής και συνεπώς η 
 , πλέον η
, πλέον η  και η
και η  .
.  παράλληλη στις
παράλληλη στις  αυτή συναντά την
αυτή συναντά την  προς τις
προς τις 
 το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  ως προς το
ως προς το 