#2
Μη αναγνωσμένη δημοσίευση
από ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ » Κυρ Απρ 29, 2018 11:03 am
sakis1963 έγραψε: ↑Πέμ Απρ 26, 2018 4:09 am
GEOMETRIA198=FB1802.png
Εστω τρίγωνο

και σημεία

της

τέτοια ώστε

.Εστω επίσης

τα έγκεντρα των τριγώνων

και

τα έγκεντρα των τριγώνων

.Αν

είναι το έγκεντρο του

και

, δείξτε ότι τα σημεία

είναι συνευθειακά.
Μπορεί να αποδειχθεί και για τυχαία σημεία  της
της  με την διαφορά οτι το
με την διαφορά οτι το  σ'αυτή την περίπτωση, είναι το έγκεντρο του τριγώνου
σ'αυτή την περίπτωση, είναι το έγκεντρο του τριγώνου 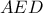
.
Ας αλλάξω τα γράμματα της εκφώνησης για δική μου ευκολία στη γενίκευση που αναφέρει ο Θάνος.
Δίνεται τρίγωνο 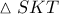 και τυχόντα σημεία
και τυχόντα σημεία  της
της 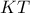 με
με  πλησιέστερο του
πλησιέστερο του  και έστω
και έστω  τα έγκεντρα των τριγώνων
τα έγκεντρα των τριγώνων  αντίστοιχα. Να δειχθεί ότι το σημείο
αντίστοιχα. Να δειχθεί ότι το σημείο 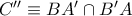 ανήκει στην
ανήκει στην  .
Απόδειξη
.
Απόδειξη
 Προφανώς
Προφανώς 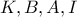 και
και  είναι συνευθειακές τετράδες ( με
είναι συνευθειακές τετράδες ( με  προφανώς το έγκεντρο του τριγώνου
προφανώς το έγκεντρο του τριγώνου 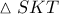 ) , σημεία των διχοτόμων των γωνιών
) , σημεία των διχοτόμων των γωνιών  αντίστοιχα. Προφανώς
αντίστοιχα. Προφανώς  και
και  συνευθειακές τριάδες (σημεία των διχοτόμων των γωνιών
συνευθειακές τριάδες (σημεία των διχοτόμων των γωνιών  αντίστοιχα) δηλαδή
αντίστοιχα) δηλαδή 
 Από (εσωτερική και εξωτερική διχοτόμο) προκύπτει ότι οι δέσμες
Από (εσωτερική και εξωτερική διχοτόμο) προκύπτει ότι οι δέσμες  είναι αρμονικές (έχουν δηλαδή ίσους διπλούς λόγους) και επειδή έχουν κοινή ακτίνα
είναι αρμονικές (έχουν δηλαδή ίσους διπλούς λόγους) και επειδή έχουν κοινή ακτίνα  τα σημεία τομής των τριών άλλων ακτινών τους είναι συνευθειακά, δηλαδή τα
τα σημεία τομής των τριών άλλων ακτινών τους είναι συνευθειακά, δηλαδή τα  είναι συνευθειακά.
είναι συνευθειακά.
 Είναι
Είναι  και
και 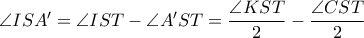 , οπότε
, οπότε 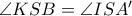 και με παρόμοιο τρόπο προκύπτει ότι
και με παρόμοιο τρόπο προκύπτει ότι 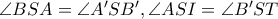 οπότε οι δέσμες
οπότε οι δέσμες  έχουν ίσες τις γωνίες των ομολόγων ακτινών τους , άρα έχουν ίσους διπλούς λόγους άρα
έχουν ίσες τις γωνίες των ομολόγων ακτινών τους , άρα έχουν ίσους διπλούς λόγους άρα  , οπότε οι ευθείες
, οπότε οι ευθείες  διέρχονται από το ίδιο σημείο και έστω
διέρχονται από το ίδιο σημείο και έστω 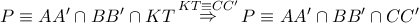

- Συνευθειακοτητα με το έγκεντρο 2.png (74.13 KiB) Προβλήθηκε 684 φορές
 Αν
Αν  , με δεδομένο ότι
, με δεδομένο ότι  σύμφωνα με το Desmic Theorem (Θεώρημα που οφείλεται σε Γάλλο γεωμέτρη που έκανε και χαλάστρα στονδικό μας Βήττα αφού προηγήθηκε σε δημοσίευση) θα ισχύει:
(α) – Οι ευθείες
σύμφωνα με το Desmic Theorem (Θεώρημα που οφείλεται σε Γάλλο γεωμέτρη που έκανε και χαλάστρα στονδικό μας Βήττα αφού προηγήθηκε σε δημοσίευση) θα ισχύει:
(α) – Οι ευθείες  τέμνονται στο ίδιο σημείο έστω
τέμνονται στο ίδιο σημείο έστω 
(β) – Οι ευθείες  τέμνονται στο ίδιο σημείο έστω
τέμνονται στο ίδιο σημείο έστω 
(γ) – Η ευθεία  διέρχεται από το σημείο
διέρχεται από το σημείο 
 Με
Με  προκύπτει σύμφωνα με το Θεώρημα Desarques ότι τα τρίγωνα
προκύπτει σύμφωνα με το Θεώρημα Desarques ότι τα τρίγωνα  είναι προοπτικά οπότε τα σημεία τομής των ομολόγων πλευρών τους θα είναι συνευθειακά, δηλαδή
είναι προοπτικά οπότε τα σημεία τομής των ομολόγων πλευρών τους θα είναι συνευθειακά, δηλαδή 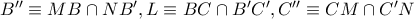 είναι συνευθειακά.
είναι συνευθειακά.
Από τις συνευθειακότητες 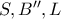 και
και  προκύπτει ότι
προκύπτει ότι  είναι συνευθειακά και το ζητούμενο έχει αποδειχθεί.
Στάθης
είναι συνευθειακά και το ζητούμενο έχει αποδειχθεί.
Στάθης.
Υ.Σ.
1. Η παραπάνω απόδειξη αφιερώνεται σε ένδειξη τιμής στον αγαπητό μου αδελφικό φίλο Κώστα Βήττα γιατί είμαι βέβαιος ότι θα την ευχαριστηθεί αφού του ταιριάζει απόλυτα.
2. Θάνο σε ευχαριστώ θερμά για την "ταλαιπωρία" που με υπέβαλες (την ευχαριστήθηκα πάρα πολύ) γιατί με έκανε να ξεχαστώ για λίγο από τα τόσα που με "κυνηγάνε" και να σου πω και δημοσίως ότι είσαι ΑΠΑΙΧΤΟΣ "συνθέτης" γεωμετρικών προβλημάτων. 
Για το Desmic Theorem δείτε
https://mathematica.gr/forum/viewtopic. ... ey#p211592 μαζί με μια απόδειξη που είχε κάνει η αφεντομουτσουνάρα μου
ΣτάθηςΤι περιμένετε λοιπόν ναρθεί , ποιόν καρτεράτε να σας σώσει.
Εσείς οι ίδιοι με τα χέρια σας , με το μυαλό σας με την πράξη αν δεν αλλάξετε τη μοίρα σας ποτέ της δεν θα αλλάξει
 και σημεία
και σημεία  της
της  τέτοια ώστε
τέτοια ώστε  .
. τα έγκεντρα των τριγώνων
τα έγκεντρα των τριγώνων  και
και  τα έγκεντρα των τριγώνων
τα έγκεντρα των τριγώνων  .
. είναι το έγκεντρο του
είναι το έγκεντρο του  και
και  , δείξτε ότι τα σημεία
, δείξτε ότι τα σημεία  είναι συνευθειακά.
είναι συνευθειακά. της
της  με την διαφορά οτι το
με την διαφορά οτι το  σ'αυτή την περίπτωση, είναι το έγκεντρο του τριγώνου
σ'αυτή την περίπτωση, είναι το έγκεντρο του τριγώνου 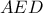 .
.
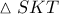 και τυχόντα σημεία
και τυχόντα σημεία  της
της 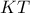 με
με  πλησιέστερο του
πλησιέστερο του  και έστω
και έστω  τα έγκεντρα των τριγώνων
τα έγκεντρα των τριγώνων  αντίστοιχα. Να δειχθεί ότι το σημείο
αντίστοιχα. Να δειχθεί ότι το σημείο 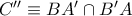 ανήκει στην
ανήκει στην  .
. 
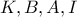 και
και  είναι συνευθειακές τετράδες ( με
είναι συνευθειακές τετράδες ( με  προφανώς το έγκεντρο του τριγώνου
προφανώς το έγκεντρο του τριγώνου  αντίστοιχα. Προφανώς
αντίστοιχα. Προφανώς  και
και  συνευθειακές τριάδες (σημεία των διχοτόμων των γωνιών
συνευθειακές τριάδες (σημεία των διχοτόμων των γωνιών  αντίστοιχα) δηλαδή
αντίστοιχα) δηλαδή 
 είναι αρμονικές (έχουν δηλαδή ίσους διπλούς λόγους) και επειδή έχουν κοινή ακτίνα
είναι αρμονικές (έχουν δηλαδή ίσους διπλούς λόγους) και επειδή έχουν κοινή ακτίνα  τα σημεία τομής των τριών άλλων ακτινών τους είναι συνευθειακά, δηλαδή τα
τα σημεία τομής των τριών άλλων ακτινών τους είναι συνευθειακά, δηλαδή τα  είναι συνευθειακά.
είναι συνευθειακά.  και
και 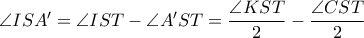 , οπότε
, οπότε 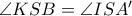 και με παρόμοιο τρόπο προκύπτει ότι
και με παρόμοιο τρόπο προκύπτει ότι 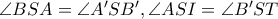 οπότε οι δέσμες
οπότε οι δέσμες  έχουν ίσες τις γωνίες των ομολόγων ακτινών τους , άρα έχουν ίσους διπλούς λόγους άρα
έχουν ίσες τις γωνίες των ομολόγων ακτινών τους , άρα έχουν ίσους διπλούς λόγους άρα  , οπότε οι ευθείες
, οπότε οι ευθείες  διέρχονται από το ίδιο σημείο και έστω
διέρχονται από το ίδιο σημείο και έστω 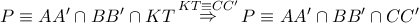
 , με δεδομένο ότι
, με δεδομένο ότι  σύμφωνα με το
σύμφωνα με το  τέμνονται στο ίδιο σημείο έστω
τέμνονται στο ίδιο σημείο έστω 
 τέμνονται στο ίδιο σημείο έστω
τέμνονται στο ίδιο σημείο έστω 
 διέρχεται από το σημείο
διέρχεται από το σημείο 
 προκύπτει σύμφωνα με το
προκύπτει σύμφωνα με το είναι προοπτικά οπότε τα σημεία τομής των ομολόγων πλευρών τους θα είναι συνευθειακά, δηλαδή
είναι προοπτικά οπότε τα σημεία τομής των ομολόγων πλευρών τους θα είναι συνευθειακά, δηλαδή 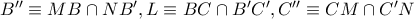 είναι συνευθειακά.
είναι συνευθειακά. 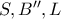 και
και  προκύπτει ότι
προκύπτει ότι  είναι συνευθειακά και το ζητούμενο έχει αποδειχθεί.
είναι συνευθειακά και το ζητούμενο έχει αποδειχθεί.