Λίγο ανορθόδοξα..
Με
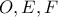
το κέντρο του κύκλου,την τομή

και κύκλου και την τομή

και κύκλου,βγαίνει απλά ότι τα

είναι ομοκυκλικά,που σημαίνει ότι

.
Τώρα,σταθεροποιώ την
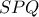
και μετακινώ το

κατά μήκος της εφαπτομένης,ενώ παράλληλα παίρνω το

ως το συμμετρικό της

ως προς την
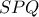
.Η ακολουθία των

και η αντίστοιχη των

δημιουργούν ίσους διπλούς λόγους στις ευθείες που κινούνται επειδή βλέπονται υπό ίσες γωνίες από το

.Με ένα απλό τσεκάρισμα,όταν το

πέσει στο

,το

πέφτει στο

επίσης.
Το τελευταίο σημαίνει ότι ο προβολικός μετασχηματισμός που συνδέει τις ακολουθίες σημείων(σημειοσειρές καλύτερα) είναι ουσιαστικά μια προοπτικότητα με σταθερό κέντρο

.
Όταν το

πέσει στο

,λόγω της διχοτόμισης της

από την

,το

θα πέσει πάνω στο

.Άρα το

είναι η τομή των

Αν πάρω για

την τομή της καθέτου από το

στην
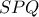
, με τον κύκλο,προκύπτει ότι

κάθετες,δηλαδή
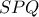
πολική του

.
Αν τώρα η άλλη εφαπτομένη από το

τέμνει τον κύκλο στο

, και η αντίστοιχη από το

στο

, με δύο Pascal,στα

προκύπτει ότι οι

συντρέχουν,δηλαδή ότι καθώς τα

μεταβάλλονται,η

περνάει από το σταθερό σημείο

.Αυτό σημαίνει ότι το σημείο

διαγράφει την πολική του

(όχι ολόκληρη απαραίτητα).Αν όμως μεταφέρω το

στην τομή των

,είναι φανερό ότι το σημείο

ταυτίζεται με το σημείο

,ενώ για

θα είναι

.Το τελευταίο αποδεικνύει το ζητούμενο...
Edit:Πώς μπορώ να βάζω φυσιολογικότερο σχήμα;
 εκτός κύκλου
εκτός κύκλου  , φέρουμε τις εφαπτόμενες και τυχούσα τέμνουσα
, φέρουμε τις εφαπτόμενες και τυχούσα τέμνουσα 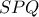 και
και  το μέσο του
το μέσο του  . Εκατέρωθεν της τέμνουσας και με κοινή πλευρά την
. Εκατέρωθεν της τέμνουσας και με κοινή πλευρά την 
 . Δείξτε ότι οι άλλες εφαπτόμενες από τα
. Δείξτε ότι οι άλλες εφαπτόμενες από τα  τέμνονται πάνω στην τέμνουσα .
τέμνονται πάνω στην τέμνουσα .
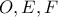 το κέντρο του κύκλου,την τομή
το κέντρο του κύκλου,την τομή  και κύκλου και την τομή
και κύκλου και την τομή  και κύκλου,βγαίνει απλά ότι τα
και κύκλου,βγαίνει απλά ότι τα  είναι ομοκυκλικά,που σημαίνει ότι
είναι ομοκυκλικά,που σημαίνει ότι 
 κατά μήκος της εφαπτομένης,ενώ παράλληλα παίρνω το
κατά μήκος της εφαπτομένης,ενώ παράλληλα παίρνω το  ως το συμμετρικό της
ως το συμμετρικό της  .
. ,λόγω της διχοτόμισης της
,λόγω της διχοτόμισης της  από την
από την  ,το
,το  .Άρα το
.Άρα το 
 κάθετες,δηλαδή
κάθετες,δηλαδή  , και η αντίστοιχη από το
, και η αντίστοιχη από το  προκύπτει ότι οι
προκύπτει ότι οι  συντρέχουν,δηλαδή ότι καθώς τα
συντρέχουν,δηλαδή ότι καθώς τα  περνάει από το σταθερό σημείο
περνάει από το σταθερό σημείο  διαγράφει την πολική του
διαγράφει την πολική του  ,είναι φανερό ότι το σημείο
,είναι φανερό ότι το σημείο  ,ενώ για
,ενώ για  θα είναι
θα είναι  .Το τελευταίο αποδεικνύει το ζητούμενο...
.Το τελευταίο αποδεικνύει το ζητούμενο... το σημείο που η εφαπτόμενη από το
το σημείο που η εφαπτόμενη από το  τότε αρκεί να ισχύει ότι
τότε αρκεί να ισχύει ότι  , έτσι ώστε
, έτσι ώστε  και
και 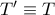 .
. ένα περιγράψιμο τετράπλευρο και έστω πως η
ένα περιγράψιμο τετράπλευρο και έστω πως η  τέμνει τον εγγεγραμμένο κύκλο στα
τέμνει τον εγγεγραμμένο κύκλο στα  . Τότε να αποδειχθεί πως
. Τότε να αποδειχθεί πως  , όπου
, όπου  (η ισοδυναμία ισχύει από τα παραπάνω).
(η ισοδυναμία ισχύει από τα παραπάνω). στα σημεία
στα σημεία  αντίστοιχα.
αντίστοιχα. και
και 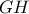 τέμνονται στο σημεία
τέμνονται στο σημεία  .
. ισχύει ότι η πολική του
ισχύει ότι η πολική του  .
. το κέντρο του κύκλου, ισχύει ότι
το κέντρο του κύκλου, ισχύει ότι  , οπότε ισχύει ότι
, οπότε ισχύει ότι 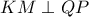 .
. τέμνει τη
τέμνει τη  .
.  είναι συνευθειακά (*).
είναι συνευθειακά (*). , τότε αφού
, τότε αφού  , θα ισχύει ότι
, θα ισχύει ότι  .
.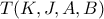 είναι αρμονική, δηλαδή αν η
είναι αρμονική, δηλαδή αν η  .
. ανήκει στην πολική του
ανήκει στην πολική του  και
και  τέμνονται στο
τέμνονται στο  (Βασικά αυτό το σημείο ταυτίζεται με το
(Βασικά αυτό το σημείο ταυτίζεται με το  στο
στο  προκύπτει πως τα σημεία
προκύπτει πως τα σημεία  είναι συνευθειακά. Από
είναι συνευθειακά. Από  παίρνουμε ότι τα
παίρνουμε ότι τα  είναι συνευθειακά. Οπότε τα
είναι συνευθειακά. Οπότε τα