 , θεωρούμε τα σημεία
, θεωρούμε τα σημεία  και
και  . Το σημείο
. Το σημείο  της ευθείας της πλευράς
της ευθείας της πλευράς  είναι τέτοιο, ώστε οι ευθείες
είναι τέτοιο, ώστε οι ευθείες  και
και  να είναι συμμετρικές ως προς τη
να είναι συμμετρικές ως προς τη  . Τα σημεία
. Τα σημεία  ,
,  ορίζονται με ανάλογο τρόπο. Να αποδείξετε ότι τα
ορίζονται με ανάλογο τρόπο. Να αποδείξετε ότι τα  ,
,  ,
,  ανήκουν στην ίδια ευθεία.
ανήκουν στην ίδια ευθεία.Συντονιστές: vittasko, silouan, Doloros
 , θεωρούμε τα σημεία
, θεωρούμε τα σημεία  και
και  . Το σημείο
. Το σημείο  της ευθείας της πλευράς
της ευθείας της πλευράς  είναι τέτοιο, ώστε οι ευθείες
είναι τέτοιο, ώστε οι ευθείες  και
και  να είναι συμμετρικές ως προς τη
να είναι συμμετρικές ως προς τη  . Τα σημεία
. Τα σημεία  ,
,  ορίζονται με ανάλογο τρόπο. Να αποδείξετε ότι τα
ορίζονται με ανάλογο τρόπο. Να αποδείξετε ότι τα  ,
,  ,
,  ανήκουν στην ίδια ευθεία.
ανήκουν στην ίδια ευθεία.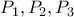 τα συμμετρικά του
τα συμμετρικά του  ως προς τις
ως προς τις  και ομοίως τα
και ομοίως τα 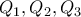 για το
για το  .Είναι γνωστό ότι οι
.Είναι γνωστό ότι οι  είναι ευθείες,οι λεγόμενες ευθείες Steiner των
είναι ευθείες,οι λεγόμενες ευθείες Steiner των  οι οποίες περνούν από το ορθόκεντρο του
οι οποίες περνούν από το ορθόκεντρο του  .
. μπορούν να οριστούν ως
μπορούν να οριστούν ως  και ως
και ως  ,δηλαδή τελικά ως
,δηλαδή τελικά ως  και ζητείται να δειχτεί ότι είναι συνευθειακά.
και ζητείται να δειχτεί ότι είναι συνευθειακά. έχουν ίσους διπλούς λόγους,γιατί τότε λόγω της κοινής τους ακτίνας, τα σημεία τομής των ομόλογων ακτινών θα είναι συνευθειακά.
έχουν ίσους διπλούς λόγους,γιατί τότε λόγω της κοινής τους ακτίνας, τα σημεία τομής των ομόλογων ακτινών θα είναι συνευθειακά.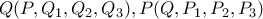 έχουν ίσους διπλούς λόγους,το οποίο όμως είναι άμεσο από τις καθετότητες(πχ.
έχουν ίσους διπλούς λόγους,το οποίο όμως είναι άμεσο από τις καθετότητες(πχ.  κλπ.,δηλαδή τελικά οι δέσμες έχουν ίσες γωνίες μεταξύ των ακτινών τους κλπ...)
κλπ.,δηλαδή τελικά οι δέσμες έχουν ίσες γωνίες μεταξύ των ακτινών τους κλπ...) ,
,  ,
,  και
και 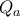 ,
,  ,
, 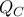 τα συμμετρικά των
τα συμμετρικά των  ,
,  ως προς τις
ως προς τις  ,
,  ,
,  αντίστοιχα.
αντίστοιχα. ,
,  ως προς το τρίγωνο
ως προς το τρίγωνο  .
. 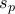 και
και  αντίστοιχα.
αντίστοιχα.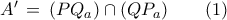 ,
, ,
,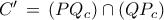
 ,
,  θεωρούμε τις παράλληλες
θεωρούμε τις παράλληλες  ,
, 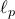 προς τις
προς τις  ,
, 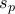 αντίστοιχα.
αντίστοιχα.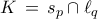 και
και 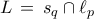 . Τότε οι πλευρές του
. Τότε οι πλευρές του  είναι παράλληλες προς τις
είναι παράλληλες προς τις  , οπότε τα δύο τρίγωνα είναι ομοιόθετα.
, οπότε τα δύο τρίγωνα είναι ομοιόθετα. ,
,  και
και 
 ότι το κέντρο
ότι το κέντρο  , δηλαδή,
, δηλαδή,  .
. και
και  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες