 με παράκεντρα τα
με παράκεντρα τα  και
και  τις προβολές τους στις
τις προβολές τους στις  αντίστοιχα.Έστω επίσης
αντίστοιχα.Έστω επίσης  τα μέσα των
τα μέσα των  .Ν.δ.ο. οι
.Ν.δ.ο. οι  συντρέχουν.
συντρέχουν.Συντονιστές: vittasko, silouan, Doloros
 με παράκεντρα τα
με παράκεντρα τα  και
και  τις προβολές τους στις
τις προβολές τους στις  αντίστοιχα.Έστω επίσης
αντίστοιχα.Έστω επίσης  τα μέσα των
τα μέσα των  .Ν.δ.ο. οι
.Ν.δ.ο. οι  συντρέχουν.
συντρέχουν. το τρίγωνο που ορίζεται από το παράκεντρα):
το τρίγωνο που ορίζεται από το παράκεντρα):  τρίγωνο και
τρίγωνο και  τα ύψη από τις κορυφές
τα ύψη από τις κορυφές  . Φέρνουμε κάθετες από τις κορυφές
. Φέρνουμε κάθετες από τις κορυφές  πάνω στις
πάνω στις  και τις τέμνουν στα
και τις τέμνουν στα 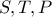 αντίστοιχα. Έστω
αντίστοιχα. Έστω  τα μέσα των
τα μέσα των  αντίστοιχα.
αντίστοιχα. συντρέχουν.
συντρέχουν. τα συμμετρικά των
τα συμμετρικά των  ως προς τις
ως προς τις  και
και  αντίστοιχα.
αντίστοιχα.  και
και  . Έστω ότι τέμνονται στο σημείο
. Έστω ότι τέμνονται στο σημείο  .
. .
. .
. , δηλαδή τα σημεία
, δηλαδή τα σημεία  είναι συνευθειακά.
είναι συνευθειακά. .
. το σημείο τομής της
το σημείο τομής της  και του περιγεγραμμένου κύκλου του
και του περιγεγραμμένου κύκλου του  και γνωρίζουμε πως από το
και γνωρίζουμε πως από το  διέρχεται και η
διέρχεται και η  .
. διέρχεται και η
διέρχεται και η  .
.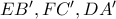 συντρέχουν.
συντρέχουν.
 και
και  τέμνονται στο
τέμνονται στο  . Εύκολα προκύπτει ότι
. Εύκολα προκύπτει ότι  , οπότε το
, οπότε το  είναι το περίκεντρο του
είναι το περίκεντρο του  .
. ισχύει ότι αφού
ισχύει ότι αφού  και
και  , είναι
, είναι 
 τα συμμετρικά των
τα συμμετρικά των  ως προς τα
ως προς τα  αντίστοιχα. Αφού και τα
αντίστοιχα. Αφού και τα  είναι τα συμμετρικά των
είναι τα συμμετρικά των  ως προς τα
ως προς τα  αντίστοιχα, είναι
αντίστοιχα, είναι 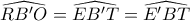 και
και  .
. .
. και
και  τέμνονται στο
τέμνονται στο  .
.  και
και  προκύπτει ότι
προκύπτει ότι  .
. ανήκει στον περιγεγραμμένο κύκλο του
ανήκει στον περιγεγραμμένο κύκλο του  (Πολλές από τις παραπάνω ισότητες γωνιών δεν ισχύουν ακριβώς, αλλά ο τελευταίος ισχυρισμός είναι αληθής).
(Πολλές από τις παραπάνω ισότητες γωνιών δεν ισχύουν ακριβώς, αλλά ο τελευταίος ισχυρισμός είναι αληθής). μπορεί να οριστεί ως η τομή της
μπορεί να οριστεί ως η τομή της  με τον περιγεγραμμένο κύκλο του
με τον περιγεγραμμένο κύκλο του  και γνωρίζουμε πως η
και γνωρίζουμε πως η  διέρχεται από αυτό το σημείο.
διέρχεται από αυτό το σημείο.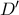 το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  , η
, η  θα διέρχεται από το
θα διέρχεται από το  .
. συντρέχουν στο
συντρέχουν στο  .
. και λόγο
και λόγο  .
. τέμνει την
τέμνει την  στο
στο  .
.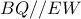 , άρα αφού
, άρα αφού  μέσο του
μέσο του  θα είναι
θα είναι  μέσο του
μέσο του  , οπότε το
, οπότε το  πάει στο
πάει στο  .
.  , δηλαδή η
, δηλαδή η  , και
, και  είναι παράλληλες (
είναι παράλληλες ( μέσα πλευρών), ισχύει ότι η
μέσα πλευρών), ισχύει ότι η  πάει στην
πάει στην  .
. πάει στην
πάει στην  και η
και η  στην
στην  .
.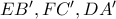 συντρέχουν στο
συντρέχουν στο  , άρα και οι
, άρα και οι  συντρέχουν στο ομοιόθετο του
συντρέχουν στο ομοιόθετο του  .
.  (ή
(ή  στο σχήμα σου) χωρίζουν σε ίσους λόγους τα ύψη (όχι απαραίτητα 1/2) το συμπέρασμα εξακολουθεί να ισχύει
στο σχήμα σου) χωρίζουν σε ίσους λόγους τα ύψη (όχι απαραίτητα 1/2) το συμπέρασμα εξακολουθεί να ισχύει  είναι ομοκυκλικές.
είναι ομοκυκλικές. είναι ομοκυκλικά.
είναι ομοκυκλικά. και δύναμης
και δύναμης 
 πάει στο
πάει στο  και αντίστροφα.
και αντίστροφα. πάει στο συμμετρικό του
πάει στο συμμετρικό του  ως προς την
ως προς την  ,έστω
,έστω  και το
και το  στο συμμετρικό του
στο συμμετρικό του  ως προς την
ως προς την  έστω
έστω  (απλό-μια ομοιότητα τριγώνων).
(απλό-μια ομοιότητα τριγώνων). πάει στο ορθόκεντρο του συμμετρικού του
πάει στο ορθόκεντρο του συμμετρικού του  ως προς την
ως προς την  έστω
έστω  .
. πάει στην τομή της κάθετης στην
πάει στην τομή της κάθετης στην  στο
στο  και της
και της  έστω
έστω  .
. πάει στο συμμετρικό του
πάει στο συμμετρικό του  ως προς το
ως προς το  ,έστω
,έστω  .
. είναι συνευθειακά,ή ισοδύναμα ότι τα
είναι συνευθειακά,ή ισοδύναμα ότι τα  ,όπου
,όπου  .
. και
και  να οριστούν ως οι τομές των
να οριστούν ως οι τομές των  ,
,  ,
, αντίστοιχα.
αντίστοιχα.
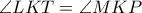 ).Από τα εγγράψιμα
).Από τα εγγράψιμα  παίρνω αντίστοιχα
παίρνω αντίστοιχα  .Έτσι τα
.Έτσι τα  είναι όμοια τρίγωνα.Θεωρώ
είναι όμοια τρίγωνα.Θεωρώ  , δύναμης
, δύναμης 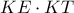 και συμμετρίας ως προς τη διχοτόμο
και συμμετρίας ως προς τη διχοτόμο  .Το
.Το  πάει στο
πάει στο  και αντίστροφα,ενώ το
και αντίστροφα,ενώ το  πάει στο
πάει στο  και αντίστροφα
και αντίστροφα  πάει λοιπόν στην ευθεία
πάει λοιπόν στην ευθεία  και ο
και ο 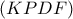 στην
στην  ,δηλαδή η τομή τους,το
,δηλαδή η τομή τους,το  , πάει στο
, πάει στο  .Επειδή το
.Επειδή το  είναι το σημείο Miquel του
είναι το σημείο Miquel του 
 θα είναι ομοκυκλικά.Επειδή το
θα είναι ομοκυκλικά.Επειδή το  είναι το σημείο Miquel του
είναι το σημείο Miquel του  τα
τα  θα είναι ομοκυκλικά.Ο
θα είναι ομοκυκλικά.Ο 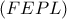 πάει στον
πάει στον  ενώ ο
ενώ ο  στον
στον  .Έτσι,η τομή των
.Έτσι,η τομή των  ,δηλαδή το
,δηλαδή το  ,πάει στην τομή των
,πάει στην τομή των  και επειδή δεν μπορεί να είναι το
και επειδή δεν μπορεί να είναι το  ,είναι το
,είναι το  .Τελικά
.Τελικά 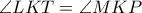
 και σημεία
και σημεία  στο επίπεδο για τα οποία ισχύει
στο επίπεδο για τα οποία ισχύει  .Οι
.Οι  συντρέχουν.
συντρέχουν. του επιπέδου,έπειτα παίρνω τη συμμετρική της
του επιπέδου,έπειτα παίρνω τη συμμετρική της 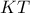 ως προς τη διχοτόμο της
ως προς τη διχοτόμο της  πάνω στην οποία επιλέγω σημείο
πάνω στην οποία επιλέγω σημείο  .Κατόπιν,παίρνω τις συμμετρικές των
.Κατόπιν,παίρνω τις συμμετρικές των  ως προς τις διχοτόμους των
ως προς τις διχοτόμους των  και οριζω ως
και οριζω ως  το σημείο τομής τους.Αρκεί να δειχτεί ότι οι
το σημείο τομής τους.Αρκεί να δειχτεί ότι οι  τέμνονται στην
τέμνονται στην  .
. κινείται στην ευθεία του (συμμετρική της
κινείται στην ευθεία του (συμμετρική της 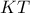 ) διαγράφει ίσο διπλό λόγο με το
) διαγράφει ίσο διπλό λόγο με το 
 ) λόγω των ίσων γωνιών.Οι δέσμες
) λόγω των ίσων γωνιών.Οι δέσμες  είναι προβολικές
είναι προβολικές  συμπέσει με το
συμπέσει με το  το
το  συμπέφτει με το
συμπέφτει με το  ,είναι και
,είναι και  πέσει στην
πέσει στην  ,το
,το  θα πέσει στην
θα πέσει στην 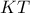 (στο ισογώνιο του
(στο ισογώνιο του  ) και όταν πέσει στη
) και όταν πέσει στη  το
το  θα βρεθεί στην
θα βρεθεί στην  .Έτσι ο άξονας προοπτικότητας (πάνω στον οποίο βρίσκονται οι τομές των ομόλογων
.Έτσι ο άξονας προοπτικότητας (πάνω στον οποίο βρίσκονται οι τομές των ομόλογων  και το ζητούμενο δείχτηκε.
και το ζητούμενο δείχτηκε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες