
- cycl_miquel.png (86.03 KiB) Προβλήθηκε 925 φορές
Το σημείο

είναι το σημείο τομής των μεσοκαθέτων των

και

,
εποµένως, είναι το ένα από τα δύο σηµεία των δύο ποδηλατιστών

για τους
κύκλους
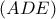
και

. Ως εκ τούτου, το

(όπου

το κέντρο του κύκλου
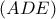
,
και

το δεύτερο κοινό σημείο των κύκλων
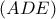
και

, που είναι το σημείο Miquel
του πλήρους τετραπλεύρου

) είναι ισοσκελές τραπέζιο.
Όμως,

(η διακεντρική ευθεία είναι κάθετη στη κοινή χορδή

), και επειδή

, τότε

.
Από την άλλη μεριά,

.
Από

και

προκύπτει ότι τα σημεία

,

και

ανήκουν στην ίδια ευθεία.
(*) (Πρόβλημα των δύο ποδηλατιστών). Δίνονται δύο κύκλοι που τέµνονται στα σηµεία A και
Τ. Δύο ποδηλάτες κινούνται σε αυτούς τους κύκλους µε σταθερές ταχύτητες και µε την ίδια
κατεύθυνση (ή και οι δύο κινούνται δεξιόστροφα, ή και οι δύο αριστερόστροφα). Αν και οι
δύο ξεκινούν ταυτόχρονα από το σηµείο Τ, και µετά από µία πλήρη περιστροφή επιστρέφουν
ταυτόχρονα στο Τ, να αποδείξετε ότι υπάρχει ένα σταθερό σηµείο του επιπέδου τέτοιο, ώστε
πάντοτε να ισαπέχει από τους δύο ποδηλάτες.
Αποδεικνύεται ότι, το σημείο των δύο ποδηλατιστών, το αντίστοιχο του σημείου

,
είναι το σημείο τομής των μεσοκαθέτων των ευθυγράμμων τμημάτων

και

.
Σε οποιοδήποτε ζεύγος τεμνόμενων κύκλων τα σημαντικά σημεία είναι δύο:
το πρώτο είναι το αντίστοιχο του σημείου

, και το δεύτερο είναι το αντίστοιχο του

.
Αυτά τα σημεία είναι συμμετρικά ως προς τη διακεντρική ευθεία των δύο κύκλων,
και η μεταξύ τους απόσταση ισούται με το μήκος της κοινής χορδής

.
Το σημείο

των δύο ποδηλατιστών, το αντίστοιχο του σημείου

,
είναι η τέταρτη κορυφή του παραλληλόγραμμου

.
Είναι επίσης, η τέταρτη κορυφή του ισοσκελούς τραπεζίου

,
που έχει ως βάσεις τις
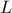
και

.
Τα παραπάνω είναι από άρθρο του B. Y. Protasof στο ρώσικο περιοδικό ΚΒΑΝΤ (2008, τεύχος 3).
 ο περίκυκλος τριγώνου
ο περίκυκλος τριγώνου  και ας είναι
και ας είναι  τυχαίος κύκλος χορδής
τυχαίος κύκλος χορδής  που τέμνει τις
που τέμνει τις  στα σημεία
στα σημεία  αντίστοιχα. Να δειχθεί ότι η
αντίστοιχα. Να δειχθεί ότι η  διέρχεται από το σημείο Miquel του πλήρους τετραπλεύρου
διέρχεται από το σημείο Miquel του πλήρους τετραπλεύρου  με
με  το αντιδιαμετρικό του
το αντιδιαμετρικό του  ως προς τον
ως προς τον 

 επί της μεσοκαθέτου της
επί της μεσοκαθέτου της  τέμνει τις
τέμνει τις  αντίστοιχα.Παίρνουμε
αντίστοιχα.Παίρνουμε  την τομή
την τομή  και
και  το αντιδιαμετρικό του
το αντιδιαμετρικό του  .Ορίζουμε
.Ορίζουμε  την τομή
την τομή  ,
,  εκείνη των
εκείνη των  και
και  το κέντρο του
το κέντρο του  .
. έχει ίδια διεύθυνση.Έπεται (Θαλής) ότι το
έχει ίδια διεύθυνση.Έπεται (Θαλής) ότι το  .Η
.Η  είναι κάθετη στην
είναι κάθετη στην  και άρα διατηρεί σταθερή διεύθυνση,δηλαδή
και άρα διατηρεί σταθερή διεύθυνση,δηλαδή 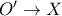 προβολική σύνδεση.Το
προβολική σύνδεση.Το  είναι η τομή του
είναι η τομή του  .Άρα
.Άρα  προβολική σύνδεση.Άρα τελικά
προβολική σύνδεση.Άρα τελικά  προβολική σύνδεση.Απ'την άλλη το
προβολική σύνδεση.Απ'την άλλη το 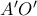 και
και  προβολική σύνδεση.Αρκεί δηλαδή να δειχτεί για 3 θέσεις του
προβολική σύνδεση.Αρκεί δηλαδή να δειχτεί για 3 θέσεις του  ταυτίζονται,κάτι που επιτυγχάνεται εύκολα αν πάρουμε
ταυτίζονται,κάτι που επιτυγχάνεται εύκολα αν πάρουμε  ,
,  και
και  ..
.. τέμνει τις
τέμνει τις  και
και  ,
,  για τους
για τους 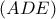 και
και  (όπου
(όπου  το κέντρο του κύκλου
το κέντρο του κύκλου  το δεύτερο κοινό σημείο των κύκλων
το δεύτερο κοινό σημείο των κύκλων  ) είναι ισοσκελές τραπέζιο.
) είναι ισοσκελές τραπέζιο. (η διακεντρική ευθεία είναι κάθετη στη κοινή χορδή
(η διακεντρική ευθεία είναι κάθετη στη κοινή χορδή  ), και επειδή
), και επειδή , τότε
, τότε  .
.  .
. και
και  προκύπτει ότι τα σημεία
προκύπτει ότι τα σημεία  .
.  .
.  ,
, 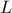 και
και  .
. και
και  οπότε αν
οπότε αν  θα είναι
θα είναι  διάμετρος του
διάμετρος του