Σε τρίγωνο
 ισχύει ότι
ισχύει ότι
Συντονιστές: vittasko, silouan, Doloros
 ισχύει ότι
ισχύει ότι
Καλησπέρα κ. Τηλέμαχε!ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Κυρ Νοέμ 17, 2019 9:43 pmΣήμερα το απόγευμα κατέληξα σε μια ανισότητα την οποία και σας προτείνω.
Σε τρίγωνοισχύει ότι

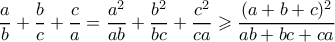 .
. και
και  (με
(με  συμβολίζω την ημιπερίμετρο)
συμβολίζω την ημιπερίμετρο) .
. , με
, με  . Είναι,
. Είναι,  , άρα η
, άρα η  είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα. , και άρα
, και άρα 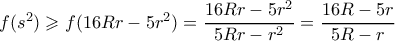 .
. (1).
(1). . Από την ανισότητα Euler,
. Από την ανισότητα Euler,  , άρα
, άρα  .
. που γράφεται
που γράφεται  , που είναι προφανής για
, που είναι προφανής για  .
.

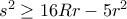


 και έτσι
και έτσι 
Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 3 επισκέπτες