Γειά σας.
Καταρχάς αλλά κυρίως Καταρχήν: Είναι καθαρό, ότι για το παραπάνω Επιστημονικό Υπέρ-Άριστο οδοιπορικό από τον Κώστα και τον Γιώργο το μόνο που έχω να πω είναι ένα τεράστιο ευχαριστώ που ασχολήθηκαν σε υψηλό επίπεδο με βάση την τριλογία που πρότεινα.
Επιτρέψτε μου τώρα την διερευνητική μου σκέψη για το
τρίτο ερώτημα με βάση την διαπραγμάτευση μου που παρουσίασα εξ αρχής και είναι η:
S.E.Louridas έγραψε: ↑Σάβ Ιαν 16, 2021 9:16 pm
Για το τρίτο τώρα ερώτημα σκέφτηκα εν τάχει ως εξής: Αν υπάρχει το σημείο επαφής

της σφαίρας με το επίπεδο

και θεωρήσουμε

τότε, ο περιγεγραμμένος κύκλος στο τρίγωνο

εφάπτεται στην ευθεία

και ο περιγεγραμμένος κύκλος στο τρίγωνο

θα εφάπτεται στην ευθεία

Άρα παίρνουμε:
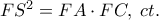
και

Επομένως προσδιορίζεται στο επίπεδο

το σημείο επαφής

ως τομή των κύκλων

και

(Είναι μάλιστα εν γένει δύο τα σημεία τομής , ως τομές δύο κύκλων, άρα τελικά εν γένει θα έχουμε αντίστοιχα δύο σφαίρες). Έτσι με βάση τα σταθερά τρίγωνα

κατασκευάζουμε την ζητούμενη σφαίρα με κέντρο την τομή των αντίστοιχων κάθετων ευθειών στα επίπεδα των τριγώνων

και στα περίκεντρα τους……
Στο διερευνηκό τώρα επίπεδο, ας δούμε τα σχήματα που ακολουθούν.
Στο σχήμα

, που είναι εύκολο να αποδείξουμε την ύπαρξη (με το

να είναι εγγεγραμμένο), συνεπικουρούμενοι από το σημείο Miquel, έστω το

δύο κύκλων

που να τέμνονται σε δύο σημεία και αυτό επειδή,



(Το τετράπλευρο

το θεωρήσαμε εγγράψιμο απλά για να πιστοποιήσουμε
την ύπαρξη τουλάχιστον μίας περίπτωσης που οι "επίμαχοι" κύκλοι τέμνονται, όπως θα διαπιστώσουμε, καθαρά σε δύο σημεία). Στο σχήμα

βλέπουμε την υπαρκτή περίπτωση οι αντίστοιχοι κύκλοι

να μην έχουν κοινό σημείο και τέλος στο σχήμα

, έχουμε τους αντίστοιχους κύκλους

που εφάπτονται.
Επειδή το επίπεδο είναι
συνεκτικός χώρος από μία τυχούσα τριάδα σημείων

, εδώ της σφαίρας, θα «πέσουμε» σε μία από τις προηγούμενες γενικές περιπτώσεις μαζί με τις περιπτώσεις στο σχήμα

ο κύκλος

να ευρίσκεται εξωτερικά του κύκλου

και ομοίως στο σχήμα

Άρα αν ισχύει η

θα έχουμε δύο σημεία τομής των «επίμαχων» κύκλων, αν

οι κύκλοι θα εφάπτονται και αν

οι κύκλοι δεν θα έχουν κοινό σημείο.

- F1.png (61.87 KiB) Προβλήθηκε 950 φορές

- F2.png (80.95 KiB) Προβλήθηκε 950 φορές

- F3.png (82.47 KiB) Προβλήθηκε 950 φορές
 και για τα σημεία
και για τα σημεία  να είναι τα
να είναι τα  ,
,  , όπου
, όπου  ,
,  ,
,  , αρκεί να παρατηρήσουμε ότι η παραβολή των σημείων που ισαπέχουν από το
, αρκεί να παρατηρήσουμε ότι η παραβολή των σημείων που ισαπέχουν από το  και από την
και από την  και η μεσοκάθετος των
και η μεσοκάθετος των  τέμνονται υποχρεωτικά σε ΔΥΟ σημεία: από τις αντίστοιχες εξισώσεις παραβολής και μεσοκαθέτου,
τέμνονται υποχρεωτικά σε ΔΥΟ σημεία: από τις αντίστοιχες εξισώσεις παραβολής και μεσοκαθέτου,  και
και  , προκύπτει για την τομή τους η δευτεροβάθμια
, προκύπτει για την τομή τους η δευτεροβάθμια
![4a_2b_2\left[(a_1-b_1)^2+(a_2-b_2)^2\right]>0. 4a_2b_2\left[(a_1-b_1)^2+(a_2-b_2)^2\right]>0.](/forum/ext/geomar/texintegr/latexrender/pictures/b44bd8af9d69660abbc2d798324f75c9.png)

 και περιέχουσες το
και περιέχουσες το  ... υπό τον όρο ότι τα
... υπό τον όρο ότι τα  κείνται εκτός του
κείνται εκτός του  να πηγάζει από το πάλαι ποτέ ρηθέν: «Αν δεν κοιτάξεις το σπίτι σου, τότε, θα πέσει και θα σε πλακώσει» (Ψυχολογία βάθους γαρ).
να πηγάζει από το πάλαι ποτέ ρηθέν: «Αν δεν κοιτάξεις το σπίτι σου, τότε, θα πέσει και θα σε πλακώσει» (Ψυχολογία βάθους γαρ). κλπ), με τον περίκυκλο του
κλπ), με τον περίκυκλο του  ): στην περίπτωση αυτή και μόνον
): στην περίπτωση αυτή και μόνον , κέντρο επί της
, κέντρο επί της  και σε απόσταση
και σε απόσταση  από το περίκεντρο του
από το περίκεντρο του  με το επίπεδο
με το επίπεδο  και θεωρήσουμε
και θεωρήσουμε  τότε, ο περιγεγραμμένος κύκλος στο τρίγωνο
τότε, ο περιγεγραμμένος κύκλος στο τρίγωνο  εφάπτεται στην ευθεία
εφάπτεται στην ευθεία  και ο περιγεγραμμένος κύκλος στο τρίγωνο
και ο περιγεγραμμένος κύκλος στο τρίγωνο  θα εφάπτεται στην ευθεία
θα εφάπτεται στην ευθεία  Άρα παίρνουμε:
Άρα παίρνουμε: 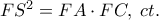 και
και  Επομένως προσδιορίζεται στο επίπεδο
Επομένως προσδιορίζεται στο επίπεδο  και
και  (Είναι μάλιστα εν γένει δύο τα σημεία τομής , ως τομές δύο κύκλων, άρα τελικά εν γένει θα έχουμε αντίστοιχα δύο σφαίρες). Έτσι με βάση τα σταθερά τρίγωνα
(Είναι μάλιστα εν γένει δύο τα σημεία τομής , ως τομές δύο κύκλων, άρα τελικά εν γένει θα έχουμε αντίστοιχα δύο σφαίρες). Έτσι με βάση τα σταθερά τρίγωνα  κατασκευάζουμε την ζητούμενη σφαίρα με κέντρο την τομή των αντίστοιχων κάθετων ευθειών στα επίπεδα των τριγώνων
κατασκευάζουμε την ζητούμενη σφαίρα με κέντρο την τομή των αντίστοιχων κάθετων ευθειών στα επίπεδα των τριγώνων  , που είναι εύκολο να αποδείξουμε την ύπαρξη (με το
, που είναι εύκολο να αποδείξουμε την ύπαρξη (με το  να είναι εγγεγραμμένο), συνεπικουρούμενοι από το σημείο Miquel, έστω το
να είναι εγγεγραμμένο), συνεπικουρούμενοι από το σημείο Miquel, έστω το  δύο κύκλων
δύο κύκλων  που να τέμνονται σε δύο σημεία και αυτό επειδή,
που να τέμνονται σε δύο σημεία και αυτό επειδή, 

 (Το τετράπλευρο
(Το τετράπλευρο  βλέπουμε την υπαρκτή περίπτωση οι αντίστοιχοι κύκλοι
βλέπουμε την υπαρκτή περίπτωση οι αντίστοιχοι κύκλοι  να μην έχουν κοινό σημείο και τέλος στο σχήμα
να μην έχουν κοινό σημείο και τέλος στο σχήμα  , έχουμε τους αντίστοιχους κύκλους
, έχουμε τους αντίστοιχους κύκλους  να ευρίσκεται εξωτερικά του κύκλου
να ευρίσκεται εξωτερικά του κύκλου  και ομοίως στο σχήμα
και ομοίως στο σχήμα 
 θα έχουμε δύο σημεία τομής των «επίμαχων» κύκλων, αν
θα έχουμε δύο σημεία τομής των «επίμαχων» κύκλων, αν  οι κύκλοι θα εφάπτονται και αν
οι κύκλοι θα εφάπτονται και αν  οι κύκλοι δεν θα έχουν κοινό σημείο.
οι κύκλοι δεν θα έχουν κοινό σημείο. ως
ως  ,
,  ,
,  'πάνω' απ' αυτό, οπότε
'πάνω' απ' αυτό, οπότε 
 και ακτίνας
και ακτίνας  είναι μόλις και μετά βίας εσωτερικός του κύκλου κέντρου
είναι μόλις και μετά βίας εσωτερικός του κύκλου κέντρου  και ακτίνας
και ακτίνας  (καθότι
(καθότι  , βλέπε και συνημμένο)^ 'αντίστοιχα', ο περίκυκλος των
, βλέπε και συνημμένο)^ 'αντίστοιχα', ο περίκυκλος των  και ακτίνα περίπου
και ακτίνα περίπου  ... άρα περνάει ΚΑΙ 'κάτω' από το επίπεδο
... άρα περνάει ΚΑΙ 'κάτω' από το επίπεδο  και
και  , θα επανέλθω!
, θα επανέλθω! έχει κέντρο περίπου στο
έχει κέντρο περίπου στο  . Ισχύει βεβαίως η ανισότητα
. Ισχύει βεβαίως η ανισότητα  , καθώς
, καθώς  . Αναφερόμενοι στο σχήμα της δημοσίευσης #11, παρατηρούμε ότι για να υπολογίσουμε το
. Αναφερόμενοι στο σχήμα της δημοσίευσης #11, παρατηρούμε ότι για να υπολογίσουμε το  οφείλουμε να προσδιορίσουμε πρώτα το
οφείλουμε να προσδιορίσουμε πρώτα το  , δηλαδή το σημείο τομής της καθέτου στο
, δηλαδή το σημείο τομής της καθέτου στο 
 ... καθότι ο περίκυκλος είναι σχεδόν κατακόρυφος (βλέπε και συνημμένο). Μπορούμε τώρα να υπολογίσουμε το
... καθότι ο περίκυκλος είναι σχεδόν κατακόρυφος (βλέπε και συνημμένο). Μπορούμε τώρα να υπολογίσουμε το 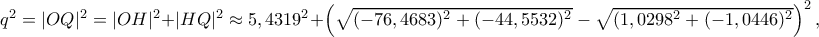
 : παρατηρούμε ότι
: παρατηρούμε ότι  , άρα όντως δεν υπάρχει η ζητούμενη σφαίρα (ΚΑΙ με το δικό μου κριτήριο).
, άρα όντως δεν υπάρχει η ζητούμενη σφαίρα (ΚΑΙ με το δικό μου κριτήριο). και δύο σημεία
και δύο σημεία  που δεν ανήκουν σε αυτό και ανήκουν στον ίδιο ημιχώρο από τους δύο που το επίπεδο
που δεν ανήκουν σε αυτό και ανήκουν στον ίδιο ημιχώρο από τους δύο που το επίπεδο  Πόσες τέτοιες σφαίρες υπάρχουν;
Πόσες τέτοιες σφαίρες υπάρχουν;
 , το σημείο τομής της
, το σημείο τομής της  με το επίπεδο
με το επίπεδο  με το μεσοκάθετο επίπεδο του τμήματος
με το μεσοκάθετο επίπεδο του τμήματος  είναι η προβολή του
είναι η προβολή του 
 στο επίπεδο
στο επίπεδο  στη σφαίρα με κέντρο το σημείο
στη σφαίρα με κέντρο το σημείο  . Τότε θα έχουμε
. Τότε θα έχουμε 
 είναι ίσο με την ακτίνα της παραπάνω σφαίρας και εφόσον
είναι ίσο με την ακτίνα της παραπάνω σφαίρας και εφόσον  είναι αρκετά απαιτητικός, όπως φάνηκε και από το παράδειγμα που έδωσα. Στην προσέγγιση του Σωτήρη δεν είναι τόσο άμεση η περιγραφή των δύο κύκλων των οποίων η ύπαρξη τομής είναι ισοδύναμη προς την ύπαρξη της ζητούμενης σφαίρας, είναι όμως σχετικά εύκολος ο προσδιορισμός των κέντρων και των ακτίνων τους. Όπως και να έχει, δεν έχουμε κατανοήσει πλήρως γιατί το να είναι ο ένας κύκλος εσωτερικός του άλλου είναι ισοδύναμο προς την (αντίστροφη) ανισότητα
είναι αρκετά απαιτητικός, όπως φάνηκε και από το παράδειγμα που έδωσα. Στην προσέγγιση του Σωτήρη δεν είναι τόσο άμεση η περιγραφή των δύο κύκλων των οποίων η ύπαρξη τομής είναι ισοδύναμη προς την ύπαρξη της ζητούμενης σφαίρας, είναι όμως σχετικά εύκολος ο προσδιορισμός των κέντρων και των ακτίνων τους. Όπως και να έχει, δεν έχουμε κατανοήσει πλήρως γιατί το να είναι ο ένας κύκλος εσωτερικός του άλλου είναι ισοδύναμο προς την (αντίστροφη) ανισότητα 
 ή τέμνονται ή είναι εσωτερικός ο ένας του άλλου^ αν όμως χρησιμοποιηθούν είτε οι δύο κύκλοι που αντιστοιχούν στα
ή τέμνονται ή είναι εσωτερικός ο ένας του άλλου^ αν όμως χρησιμοποιηθούν είτε οι δύο κύκλοι που αντιστοιχούν στα  είτε οι δύο κύκλοι που αντιστοιχούν στα
είτε οι δύο κύκλοι που αντιστοιχούν στα  ,
,  ,
,  , όπου, αναμενόμενα, οι τρεις κύκλοι τέμνονται στα ίδια σημεία (κέντρα των δύο εφαπτόμενων σφαιρών).
, όπου, αναμενόμενα, οι τρεις κύκλοι τέμνονται στα ίδια σημεία (κέντρα των δύο εφαπτόμενων σφαιρών).