Συμβολίζουμε με

το σημείο τομής των

και

, και

τον περιγεγραμμένο κύκλο του

.
Έστω

το σημείο επαφής του κύκλου

με το τόξο

του

,

το μέσο του τόξου

του

.
Η ευθεία

διέρχεται από το

. Η ευθεία

διέρχεται από το

(Λήμμα Αρχιμήδη).
Οι γωνίες

και

είναι ίσες (Οι αντίστοιχες επίκεντρες

,

στους κύκλους

,

αντίστοιχα,
είναι ίσες, ως εντός εναλλάξ των παραλλήλων

και

που τέμνονται από την

).
Ως εκ τούτου, προκύπτει ότι τα σημεία

,

,

,

ανήκουν στον ίδιο κύκλο, και επομένως

.

- Sharygin.png (45.51 KiB) Προβλήθηκε 596 φορές
Επιπλέον,

(ιδιότητα έγκεντρου τριγώνου). Τα τρίγωνα

και

είναι όμοια (

,

).
Επομένως,

. Από αυτό προκύπτει ότι, τα τρίγωνα
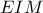
και

είναι όμοια.
Ως εκ τούτου

, από το οποίο προκύπτει η επαφή της

με τον κύκλο

.
Τώρα, εύκολα αποδεικνύεται ότι η παράλληλη από το

της

εφάπτεται του εγγεγραμμένου κύκλου

του τριγώνου

.
Πράγματι,

(το τρίγωνο

ισοσκελές).
Λόγω της παραλληλίας

είναι

.
Επομένως, η

διχοτόμος της γωνίας

, και εφόσον ο κύκλος

εφάπτεται της

,
θα εφάπτεται και της

.
Υ.Γ. Όπως αναφέρει ο συγγραφέας η μέθοδος απόδειξης είναι του Β. Γ. Προτασόφ (Γνωστός Ρώσος Γεωμέτρης από τα πολλά άρθρα
που έχει συγγράψει για το περιοδικό ΚΒΑΝΤ).
 που εφάπτεται της πλευράς
που εφάπτεται της πλευράς  τριγώνου
τριγώνου  σε σημείο
σε σημείο  και του περιγεγραμμένου κύκλου του
και του περιγεγραμμένου κύκλου του  (το σημείο επαφής στο τόξο
(το σημείο επαφής στο τόξο  ). Η ευθεία
). Η ευθεία  , όπου
, όπου  το έγκεντρο του τριγώνου
το έγκεντρο του τριγώνου  , τέμνει για δεύτερη φορά τον κύκλο
, τέμνει για δεύτερη φορά τον κύκλο  στο σημείο
στο σημείο  . Να αποδείξετε ότι η ευθεία
. Να αποδείξετε ότι η ευθεία  εφάπτεται του
εφάπτεται του  . Στη συνέχεια, να αποδείξετε ότι η παράλληλη από το
. Στη συνέχεια, να αποδείξετε ότι η παράλληλη από το  της
της  εφάπτεται του εγγεγραμμένου κύκλου
εφάπτεται του εγγεγραμμένου κύκλου  του
του  .
.
 α) Έστω
α) Έστω  Η εφαπτόμενη στον κύκλο
Η εφαπτόμενη στον κύκλο  κέντρου
κέντρου  (που εφάπτεται στον περίκυκλο
(που εφάπτεται στον περίκυκλο  του τριγώνου
του τριγώνου  στο
στο  και στην πλευρά του
και στην πλευρά του  η διχοτόμος της γωνίας
η διχοτόμος της γωνίας  (προφανώς το
(προφανώς το  είναι το μέσο του τόξου
είναι το μέσο του τόξου  ) και αρκεί ως ισοδύναμο πρόβλημα να δείξουμε ότι το
) και αρκεί ως ισοδύναμο πρόβλημα να δείξουμε ότι το  να ταυτίζεται με το έγκεντρο του τριγώνου
να ταυτίζεται με το έγκεντρο του τριγώνου 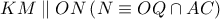 (κάθετες στην
(κάθετες στην  συνευθειακά (οι
συνευθειακά (οι  εφάπτονται στο
εφάπτονται στο  συνευθειακά.
συνευθειακά.  , με
, με  (έχουν μια κοινή γωνία την
(έχουν μια κοινή γωνία την  ) θα είναι
) θα είναι 
 ομοκυκλικά και συνεπώς
ομοκυκλικά και συνεπώς  εφαπτόμενο τμήμα στον περίκυκλο του τριγώνου
εφαπτόμενο τμήμα στον περίκυκλο του τριγώνου  και με
και με 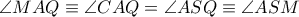 (τα τόξα
(τα τόξα  είναι ίσα από τη διχοτόμο
είναι ίσα από τη διχοτόμο  ) προκύπτει ότι
) προκύπτει ότι  εφαπτόμενο τμήμα στον περίκυκλο του τριγώνου
εφαπτόμενο τμήμα στον περίκυκλο του τριγώνου  και συνεπώς (αφού το
και συνεπώς (αφού το  το δεύτερο (εκτός του
το δεύτερο (εκτός του  ) εφαπτόμενο τμήμα του
) εφαπτόμενο τμήμα του  από το
από το  .
. τότε
τότε  (εφαπτόμενα τμήματα του
(εφαπτόμενα τμήματα του 
 (εντός εναλλάξ...) και το ισοδύναμο του β) ζητουμένου έχει αποδειχθεί .
(εντός εναλλάξ...) και το ισοδύναμο του β) ζητουμένου έχει αποδειχθεί .  το σημείο τομής των
το σημείο τομής των  τον περιγεγραμμένο κύκλο του
τον περιγεγραμμένο κύκλο του  το σημείο επαφής του κύκλου
το σημείο επαφής του κύκλου  το μέσο του τόξου
το μέσο του τόξου  διέρχεται από το
διέρχεται από το  διέρχεται από το
διέρχεται από το  και
και  είναι ίσες (Οι αντίστοιχες επίκεντρες
είναι ίσες (Οι αντίστοιχες επίκεντρες  ,
,  στους κύκλους
στους κύκλους  και
και  που τέμνονται από την
που τέμνονται από την  ).
).  ,
,  .
.  (ιδιότητα έγκεντρου τριγώνου). Τα τρίγωνα
(ιδιότητα έγκεντρου τριγώνου). Τα τρίγωνα  και
και  είναι όμοια (
είναι όμοια ( ,
,  ).
).  . Από αυτό προκύπτει ότι, τα τρίγωνα
. Από αυτό προκύπτει ότι, τα τρίγωνα 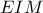 και
και  είναι όμοια.
είναι όμοια.  , από το οποίο προκύπτει η επαφή της
, από το οποίο προκύπτει η επαφή της  εφάπτεται του εγγεγραμμένου κύκλου
εφάπτεται του εγγεγραμμένου κύκλου  (το τρίγωνο
(το τρίγωνο  ισοσκελές).
ισοσκελές). είναι
είναι  .
.  διχοτόμος της γωνίας
διχοτόμος της γωνίας  , και εφόσον ο κύκλος
, και εφόσον ο κύκλος  ,
, .
.