Συνευθειακά σημεία
Συντονιστές: vittasko, silouan, Doloros
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Συνευθειακά σημεία
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Σάβ Φεβ 24, 2024 2:45 am, έχει επεξεργασθεί 1 φορά συνολικά.
Λέξεις Κλειδιά:
- vittasko
- Επιμελητής
- Δημοσιεύσεις: 2230
- Εγγραφή: Πέμ Ιαν 08, 2009 8:46 am
- Τοποθεσία: Μαρούσι - Αθήνα.
- Επικοινωνία:
Re: Συνευθειακά σημεία
Το πρόβλημα αληθεύει για τυχόντες κύκλους που εφάπτονται των πλευρών των γωνιών 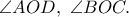
Θα αποδειχθεί η γενίκευση με την παρακάτω εκφώνηση:
Δίνεται τετράπλευρο εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  και έστω το σημείο
και έστω το σημείο 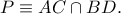 Έστω
Έστω  δύο τυχόντες κύκλοι οι οποίοι εφάπτονται των πλευρών των γωνιών
δύο τυχόντες κύκλοι οι οποίοι εφάπτονται των πλευρών των γωνιών 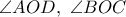 , με
, με  το κέντρο του
το κέντρο του  Αποδείξτε ότι το εσωτερικό κέντρο ομοιοθεσίας των κύκλων
Αποδείξτε ότι το εσωτερικό κέντρο ομοιοθεσίας των κύκλων  ανήκει στην ευθεία
ανήκει στην ευθεία 
 'Εστω
'Εστω 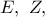 τα σημεία επαφής των κύκλων
τα σημεία επαφής των κύκλων  αντιστοίχως, στην μία κοινή τους εσωτερική εφαπτομένη και έστω το σημείο
αντιστοίχως, στην μία κοινή τους εσωτερική εφαπτομένη και έστω το σημείο 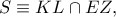 με
με  την διάκεντρο των κύκλων.
Από
την διάκεντρο των κύκλων.
Από 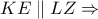
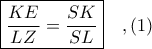
Έστω το σημείο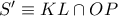 και ας είναι
και ας είναι 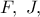 οι προβολές των
οι προβολές των  αντιστοίχως, επί της ευθείας
αντιστοίχως, επί της ευθείας 
Από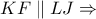
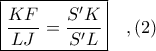
Από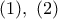 για να είναι
για να είναι 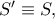 αρκεί να αποδειχθεί ότι ισχύει
αρκεί να αποδειχθεί ότι ισχύει 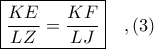
 Στο ισοσκελές τρίγωνο
Στο ισοσκελές τρίγωνο  με το σημείο
με το σημείο  στο εσωτερικό του και επί των μεσοκαθέτων ευθείων
στο εσωτερικό του και επί των μεσοκαθέτων ευθείων 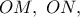 των πλευρών
των πλευρών  αντιστοίχως, για τις οποίες ισχύει προφανώς
αντιστοίχως, για τις οποίες ισχύει προφανώς  και
και 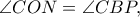 θεωρούμε ως τυχόντα τα σημεία
θεωρούμε ως τυχόντα τα σημεία 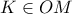 και
και 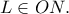
Σύμφωνα με το παρακάτω Λήμμα 1, αληθεύει η και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.
ΛΗΜΜΑ 1. Δίνεται ισοσκελές τρίγωνο με
με  και έστω
και έστω  τυχόν σημείο στο εσωτερικό του. Έστω
τυχόν σημείο στο εσωτερικό του. Έστω  δύο ευθείες δια της κορυφής
δύο ευθείες δια της κορυφής  και προς το εξωτερικό μέρος του
και προς το εξωτερικό μέρος του  έτσι ώστε να είναι
έτσι ώστε να είναι  και
και  Έστω τα τυχόντα σημεία
Έστω τα τυχόντα σημεία 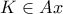 και
και 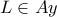 και ας είναι
και ας είναι  οι προβολές του
οι προβολές του  επί των
επί των 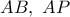 αντιστοίχως και
αντιστοίχως και 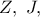 οι προβολές του
οι προβολές του  επί των
επί των 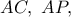 αντιστοίχως. Αποδείξτε ότι
αντιστοίχως. Αποδείξτε ότι 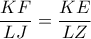 .
.
Κώστας Βήττας.
ΥΓ. Θα βάλω αργότερα την απόδειξη που έχω υπόψη μου για το ως άνω Λήμμα 1.
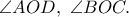
Θα αποδειχθεί η γενίκευση με την παρακάτω εκφώνηση:
Δίνεται τετράπλευρο
 εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  και έστω το σημείο
και έστω το σημείο 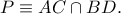 Έστω
Έστω  δύο τυχόντες κύκλοι οι οποίοι εφάπτονται των πλευρών των γωνιών
δύο τυχόντες κύκλοι οι οποίοι εφάπτονται των πλευρών των γωνιών 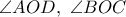 , με
, με  το κέντρο του
το κέντρο του  Αποδείξτε ότι το εσωτερικό κέντρο ομοιοθεσίας των κύκλων
Αποδείξτε ότι το εσωτερικό κέντρο ομοιοθεσίας των κύκλων  ανήκει στην ευθεία
ανήκει στην ευθεία 
 'Εστω
'Εστω 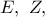 τα σημεία επαφής των κύκλων
τα σημεία επαφής των κύκλων  αντιστοίχως, στην μία κοινή τους εσωτερική εφαπτομένη και έστω το σημείο
αντιστοίχως, στην μία κοινή τους εσωτερική εφαπτομένη και έστω το σημείο 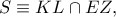 με
με  την διάκεντρο των κύκλων.
Από
την διάκεντρο των κύκλων.
Από 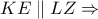
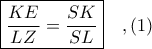
Έστω το σημείο
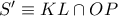 και ας είναι
και ας είναι 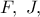 οι προβολές των
οι προβολές των  αντιστοίχως, επί της ευθείας
αντιστοίχως, επί της ευθείας 
Από
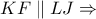
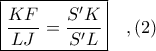
Από
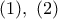 για να είναι
για να είναι 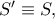 αρκεί να αποδειχθεί ότι ισχύει
αρκεί να αποδειχθεί ότι ισχύει 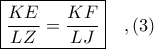
 Στο ισοσκελές τρίγωνο
Στο ισοσκελές τρίγωνο  με το σημείο
με το σημείο  στο εσωτερικό του και επί των μεσοκαθέτων ευθείων
στο εσωτερικό του και επί των μεσοκαθέτων ευθείων 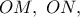 των πλευρών
των πλευρών  αντιστοίχως, για τις οποίες ισχύει προφανώς
αντιστοίχως, για τις οποίες ισχύει προφανώς  και
και 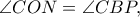 θεωρούμε ως τυχόντα τα σημεία
θεωρούμε ως τυχόντα τα σημεία 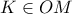 και
και 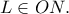
Σύμφωνα με το παρακάτω Λήμμα 1, αληθεύει η
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.ΛΗΜΜΑ 1. Δίνεται ισοσκελές τρίγωνο
 με
με  και έστω
και έστω  τυχόν σημείο στο εσωτερικό του. Έστω
τυχόν σημείο στο εσωτερικό του. Έστω  δύο ευθείες δια της κορυφής
δύο ευθείες δια της κορυφής  και προς το εξωτερικό μέρος του
και προς το εξωτερικό μέρος του  έτσι ώστε να είναι
έτσι ώστε να είναι  και
και  Έστω τα τυχόντα σημεία
Έστω τα τυχόντα σημεία 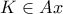 και
και 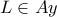 και ας είναι
και ας είναι  οι προβολές του
οι προβολές του  επί των
επί των 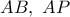 αντιστοίχως και
αντιστοίχως και 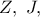 οι προβολές του
οι προβολές του  επί των
επί των 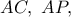 αντιστοίχως. Αποδείξτε ότι
αντιστοίχως. Αποδείξτε ότι 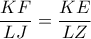 .
.Κώστας Βήττας.
ΥΓ. Θα βάλω αργότερα την απόδειξη που έχω υπόψη μου για το ως άνω Λήμμα 1.
- vittasko
- Επιμελητής
- Δημοσιεύσεις: 2230
- Εγγραφή: Πέμ Ιαν 08, 2009 8:46 am
- Τοποθεσία: Μαρούσι - Αθήνα.
- Επικοινωνία:
Re: Συνευθειακά σημεία
vittasko έγραψε: ↑Πέμ Ιουν 29, 2023 9:59 pmΛΗΜΜΑ 1. Δίνεται ισοσκελές τρίγωνομε
και έστω
τυχόν σημείο στο εσωτερικό του. Έστω
δύο ευθείες δια της κορυφής
και προς το εξωτερικό μέρος του
έτσι ώστε να είναι
και
Έστω τα τυχόντα σημεία
και
και ας είναι
οι προβολές του
επί των
αντιστοίχως και
οι προβολές του
επί των
αντιστοίχως. Αποδείξτε ότι
.
 Έστω
Έστω  η προβολή του σημείου
η προβολή του σημείου  επί της πλευράς
επί της πλευράς 
Από τα όμοια ορθογώνια τρίγωνα
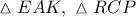 έχουμε
έχουμε 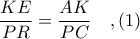
Από τα όμοια ορθογώνια τρίγωνα
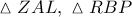 έχουμε
έχουμε 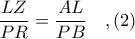
Από
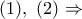
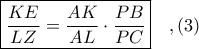
 Η δια του σημείου
Η δια του σημείου  παράλληλη ευθεία προς την
παράλληλη ευθεία προς την  τέμνει την
τέμνει την  στο σημείο έστω
στο σημείο έστω  και σύμφωνα με το παρακάτω Λήμμα2, έχουμε
και σύμφωνα με το παρακάτω Λήμμα2, έχουμε 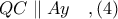
Από το ορθογώνιο τρίγωνο
 έχουμε
έχουμε 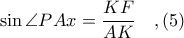
Από το ορθογώνιο τρίγωνο
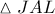 έχουμε
έχουμε 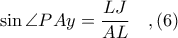
Από

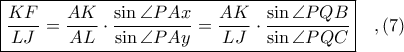
 Από τα τρίγωνα
Από τα τρίγωνα 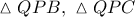 με κοινή πλευρά την
με κοινή πλευρά την  και
και 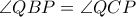 λόγω του ισοσκελούς τριγώνου
λόγω του ισοσκελούς τριγώνου  ,
, προκύπτει εύκολα ότι
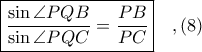
Από
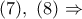
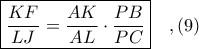
Από
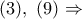
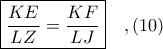 και το Λήμμα 1 έχει αποδειχθεί.
και το Λήμμα 1 έχει αποδειχθεί.ΛΗΜΜΑ 2. Δίνεται ισοσκελές τρίγωνο
 με
με  και έστω
και έστω  τυχόν σημείο στο εσωτερικό του. Δια των σημείων
τυχόν σημείο στο εσωτερικό του. Δια των σημείων 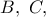 φέρνουμε τις ευθείες
φέρνουμε τις ευθείες  αντιστοίχως, έτσι ώστε να είναι
αντιστοίχως, έτσι ώστε να είναι 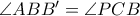 και
και 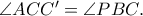 Αποδείξτε ότι τα σημεία
Αποδείξτε ότι τα σημεία 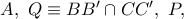 είναι συνευθειακά.
είναι συνευθειακά.Κώστας Βήττας.
ΥΓ. Θα βάλω αργότερα την απόδειξη που έχω υπόψη μου, για το ως άνω Λήμμα 2.
- vittasko
- Επιμελητής
- Δημοσιεύσεις: 2230
- Εγγραφή: Πέμ Ιαν 08, 2009 8:46 am
- Τοποθεσία: Μαρούσι - Αθήνα.
- Επικοινωνία:
Re: Συνευθειακά σημεία
Έστω το σημείο
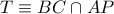 και ας είναι
και ας είναι 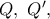 τα σημεία τομής της ευθείας
τα σημεία τομής της ευθείας  από τις ευθείες
από τις ευθείες 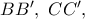 αντιστοίχως.
αντιστοίχως.Οι δέσμες
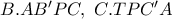 τέμνονται από την ευθεία
τέμνονται από την ευθεία  και άρα έχουμε:
και άρα έχουμε: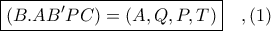 και
και 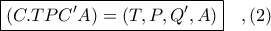
Από
 και
και 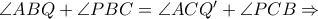
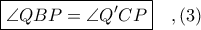 Ισχύει
Ισχύει 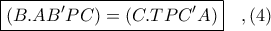 λόγω της
λόγω της  .
.( Οι δέσμες έχουν ίσους Διπλούς λόγους γιατί οι ομόλογες ευθείες τους σχηματίζουν ίσες γωνίες ).
Από
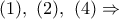
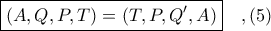
Αλλά
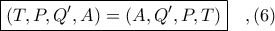
( ο Διπλός λόγος δεν μεταβάλεται εάν δύο στοιχεία μέσα στην παρένθεση αλλάξουν θέση μεταξύ τους και ταυτόχρονα αλλάξουν θέση μεταξύ τους και τα άλλα δύο στοιχεία ).
Από

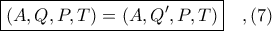
Από
 συμπεραίνεται ότι
συμπεραίνεται ότι 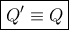 και το Λήμμα 2 έχει αποδειχθεί.
και το Λήμμα 2 έχει αποδειχθεί.Κώστας Βήττας.
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Re: Συνευθειακά σημεία
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Σάβ Φεβ 24, 2024 2:44 am, έχει επεξεργασθεί 1 φορά συνολικά.
- vittasko
- Επιμελητής
- Δημοσιεύσεις: 2230
- Εγγραφή: Πέμ Ιαν 08, 2009 8:46 am
- Τοποθεσία: Μαρούσι - Αθήνα.
- Επικοινωνία:
Re: Συνευθειακά σημεία
Ορέστη, σ' ευχαριστώ πολύ. Όσο θα μπορούμε να λύνουμε κάποια γεωμετρικά προβλήματα, θα είμαστε καλά. Ελπίζω αυτό να είναι εφικτό μέχρι τα 103, όπως έχουμε πει με τον αδελφικό μου φίλο Νίκο Φραγκάκη (...μέχρι τα εκατόν τρία θα κάνουμε Γεωμετρία).
Οι τριγωνομετρικές εκφράσεις μπορούν να παραλειφθούν και να πάμε από τηνvittasko έγραψε: ↑Πέμ Ιουν 29, 2023 9:59 pmΛΗΜΜΑ 1. Δίνεται ισοσκελές τρίγωνομε
και έστω
τυχόν σημείο στο εσωτερικό του. Έστω
δύο ευθείες δια της κορυφής
και προς το εξωτερικό μέρος του
έτσι ώστε να είναι
και
Έστω τα τυχόντα σημεία
και
και ας είναι
οι προβολές του
επί των
αντιστοίχως και
οι προβολές του
επί των
αντιστοίχως. Αποδείξτε ότι
.
 στην
στην  με συνθετικό τρόπο.
με συνθετικό τρόπο. Έστω
Έστω  η προβολή του σημείου
η προβολή του σημείου  επί της πλευράς
επί της πλευράς 
Από τα όμοια ορθογώνια τρίγωνα
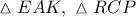 έχουμε
έχουμε 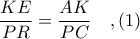
Από τα όμοια ορθογώνια τρίγωνα
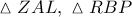 έχουμε
έχουμε 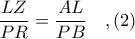
Από
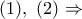
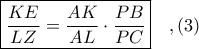
Η δια του σημείου
 παράλληλη ευθεία προς την
παράλληλη ευθεία προς την  τέμνει την
τέμνει την  στο σημείο έστω
στο σημείο έστω  και σύμφωνα με το παρακάτω Λήμμα2, έχουμε
και σύμφωνα με το παρακάτω Λήμμα2, έχουμε 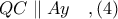
 Έστω
Έστω  οι προβολές του σημείου
οι προβολές του σημείου  επί των
επί των 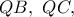 αντιστοίχως.
αντιστοίχως.Από τα όμοια ορθογώνια τρίγωνα
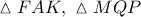 έχουμε
έχουμε 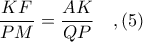
Από τα όμοια ορθογώνια τρίγωνα
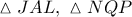 έχουμε
έχουμε 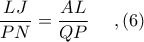
Από

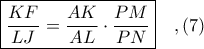
Από τα όμοια ορθογώνια τρίγωνα
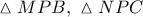 έχουμε
έχουμε 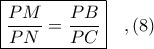
Από
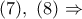
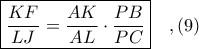
Από
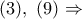
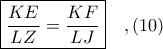 και το Λήμμα 1 έχει αποδειχθεί.
και το Λήμμα 1 έχει αποδειχθεί.Κώστας Βήττας.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
