 του τριγώνου
του τριγώνου  είναι και το έγκεντρο του τριγώνου
είναι και το έγκεντρο του τριγώνου  . Το σημείο
. Το σημείο  είναι το περίκεντρο του τριγώνου
είναι το περίκεντρο του τριγώνου  . Να αποδείξετε ότι οι ευθείες
. Να αποδείξετε ότι οι ευθείες  ,
,  και
και  διέρχονται από το ίδιο σημείο.
διέρχονται από το ίδιο σημείο.
Συντονιστές: vittasko, silouan, Doloros
 του τριγώνου
του τριγώνου  είναι και το έγκεντρο του τριγώνου
είναι και το έγκεντρο του τριγώνου  . Το σημείο
. Το σημείο  είναι το περίκεντρο του τριγώνου
είναι το περίκεντρο του τριγώνου  . Να αποδείξετε ότι οι ευθείες
. Να αποδείξετε ότι οι ευθείες  ,
,  και
και  διέρχονται από το ίδιο σημείο.
διέρχονται από το ίδιο σημείο.
 ,
,  και
και 
 και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  Είναι
Είναι 


 ,
, 

 και
και  τέμνονται στο σημείο
τέμνονται στο σημείο 

 και
και 
 και αφού
και αφού  ,
, 



 και αφού
και αφού  με τα
με τα  προς το ίδιο μέρος του
προς το ίδιο μέρος του  ως προς την ευθεία
ως προς την ευθεία  , έπεται ότι
, έπεται ότι  και η απόδειξη τελείωσε.
και η απόδειξη τελείωσε.Καλησπέρα Γιάννη και Κώσταgiannimani έγραψε: ↑Σάβ Νοέμ 04, 2023 11:37 pmΈστω ότι το ορθόκεντροτου τριγώνου
είναι και το έγκεντρο του τριγώνου
. Το σημείο
είναι το περίκεντρο του τριγώνου
. Να αποδείξετε ότι οι ευθείες
,
και
διέρχονται από το ίδιο σημείο.
orthoc_incent .png
 Ας είναι
Ας είναι  τα ύψη του τριγώνου
τα ύψη του τριγώνου  ,
,  τα σημεία επαφής του έγκυκλου
τα σημεία επαφής του έγκυκλου  του
του  και
και  το μέσο της
το μέσο της  (προφανώς το κέντρο του κύκλου του περιγεγραμμένου τετραπλεύρου
(προφανώς το κέντρο του κύκλου του περιγεγραμμένου τετραπλεύρου  (λόγω των ορθών γωνιών (από τα ύψη)))
(λόγω των ορθών γωνιών (από τα ύψη))) Από τα ομοκυκλικά σημεία
Από τα ομοκυκλικά σημεία  σε κύκλο διαμέτρου
σε κύκλο διαμέτρου  (λόγω των ορθών γωνιών) προκύπτει ότι
(λόγω των ορθών γωνιών) προκύπτει ότι  συνευθειακά και με ακριβώς όμοιο τρόπο προκύπτει ότι και
συνευθειακά και με ακριβώς όμοιο τρόπο προκύπτει ότι και 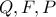 συνευθειακά και ας είναι
συνευθειακά και ας είναι  το σημείο τομής της ευθείας
το σημείο τομής της ευθείας 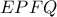 με την
με την 
 Από τα εφαπτομενικά στον
Από τα εφαπτομενικά στον  τμήματα
τμήματα 
 Από το Θεώρημα του Nagel είναι γνωστό ότι και
Από το Θεώρημα του Nagel είναι γνωστό ότι και 
 Από το πλήρες τετράπλευρο
Από το πλήρες τετράπλευρο  με κορμό
με κορμό  εγγεγραμμένο στον κύκλο
εγγεγραμμένο στον κύκλο 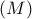 προκύπτει (γνωστότατη πρόταση (άλλωστε η
προκύπτει (γνωστότατη πρόταση (άλλωστε η  είναι η πολική του
είναι η πολική του  ως προς τον κύκλο
ως προς τον κύκλο 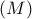 ) ότι
) ότι  (μάλιστα το σημείο τομής τους είναι το σημείο Miquel του πλήρους αυτού τετραπλεύρου
(μάλιστα το σημείο τομής τους είναι το σημείο Miquel του πλήρους αυτού τετραπλεύρου Από
Από  το ορθόκεντρο (σημείο τομής δύο υψών) και του τριγώνου
το ορθόκεντρο (σημείο τομής δύο υψών) και του τριγώνου  , οπότε
, οπότε 
 (όπως ορίστηκε) βρίσκεται επί της πολικής
(όπως ορίστηκε) βρίσκεται επί της πολικής  του
του  ως προς τον
ως προς τον  και συνεπώς
και συνεπώς  είναι αρμονική δέσμη , όπου
είναι αρμονική δέσμη , όπου  με
με  είναι τα σημεία τομής της
είναι τα σημεία τομής της  με τον κύκλο
με τον κύκλο  και την ευθεία
και την ευθεία  αντίστοιχα και με
αντίστοιχα και με  εφαπτόμενη του
εφαπτόμενη του  προκύπτει ότι
προκύπτει ότι  είναι η πολική του
είναι η πολική του  ως προς τον
ως προς τον  , άρα
, άρα 
 Από
Από  και με δεδομένο ότι
και με δεδομένο ότι  (κάθετες στην
(κάθετες στην  ) προκύπτει ότι τα τρίγωνα
) προκύπτει ότι τα τρίγωνα  έχουν τις πλευρές τους παράλληλες μια προς μία, άρα είναι όμοια (και ομοιόθετα) και οι ευθείες που συνδέουν τις ομόλογες κορυφές τους θα διέρχονται από το ίδιο σημείο , δηλαδή
έχουν τις πλευρές τους παράλληλες μια προς μία, άρα είναι όμοια (και ομοιόθετα) και οι ευθείες που συνδέουν τις ομόλογες κορυφές τους θα διέρχονται από το ίδιο σημείο , δηλαδή  και το ζητούμενο έχει αποδειχθεί .
και το ζητούμενο έχει αποδειχθεί . και
και  είναι ομοιόθετα και τότε παίρνουμε το ζητούμενο.
είναι ομοιόθετα και τότε παίρνουμε το ζητούμενο.  και
και 
 προκύπτει
προκύπτει  και είναι γνωστό πως
και είναι γνωστό πως  , οπότε αρκεί νδο
, οπότε αρκεί νδο  ή ισοδύναμα αρκεί νδο
ή ισοδύναμα αρκεί νδο  Θα το πάμε με bashing που βγαίνει ανώδυνα.
Θα το πάμε με bashing που βγαίνει ανώδυνα.




 που ισχύει...
που ισχύει...Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες