 ειναι ακεραιοι, ετσι ωστε
ειναι ακεραιοι, ετσι ωστε  ειναι επισης ακεπαραιος αριθμος. Να αποδειξειτε οτι
ειναι επισης ακεπαραιος αριθμος. Να αποδειξειτε οτι  ειναι τελειος κυβος.
ειναι τελειος κυβος.Δατης Καλαλη Γ'γυμνασιου, Κυπρος
Συντονιστές: cretanman, silouan, rek2
 ειναι ακεραιοι, ετσι ωστε
ειναι ακεραιοι, ετσι ωστε  ειναι επισης ακεπαραιος αριθμος. Να αποδειξειτε οτι
ειναι επισης ακεπαραιος αριθμος. Να αποδειξειτε οτι  ειναι τελειος κυβος.
ειναι τελειος κυβος. . Έστω
. Έστω  πρώτος και έστω
πρώτος και έστω  η δύναμη του
η δύναμη του  στην παραγοντοποίηση του
στην παραγοντοποίηση του  .
.  . Προφανώς
. Προφανώς  και
και 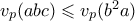 .
. . Οπότε
. Οπότε  .
.  . Προφανώς
. Προφανώς 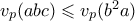 .
. τότε θα έχουμε είτε
τότε θα έχουμε είτε  είτε
είτε  . Για να ισχύει λοιπόν
. Για να ισχύει λοιπόν  θα πρέπει να έχουμε
θα πρέπει να έχουμε  .
. είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  για κάθε
για κάθε  και το
και το  είναι τέλειος κύβος.
είναι τέλειος κύβος.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης