 ειναι θετικοι ακεραιοι ετσι ωστε
ειναι θετικοι ακεραιοι ετσι ωστε  . Να αποδειξειτε οτι υπαρχει απειροι πρωτοι αριθμοι
. Να αποδειξειτε οτι υπαρχει απειροι πρωτοι αριθμοι  , ετσι ωστε υπαρχουν τουλαχιστον ενας θετικος ακεραιος
, ετσι ωστε υπαρχουν τουλαχιστον ενας θετικος ακεραιος  , για τον οποια ισχυει,
, για τον οποια ισχυει, 
Συντονιστές: cretanman, silouan, rek2
 ειναι θετικοι ακεραιοι ετσι ωστε
ειναι θετικοι ακεραιοι ετσι ωστε  . Να αποδειξειτε οτι υπαρχει απειροι πρωτοι αριθμοι
. Να αποδειξειτε οτι υπαρχει απειροι πρωτοι αριθμοι  , ετσι ωστε υπαρχουν τουλαχιστον ενας θετικος ακεραιος
, ετσι ωστε υπαρχουν τουλαχιστον ενας θετικος ακεραιος  , για τον οποια ισχυει,
, για τον οποια ισχυει, 
 ισούται με
ισούται με  . (Αν
. (Αν  ο μέγιστος κοινός διαιρέτης τότε εργαζόμαστε με τους
ο μέγιστος κοινός διαιρέτης τότε εργαζόμαστε με τους  και
και  .
. .
. για κάποιον αρκετά μεγάλο πρώτο αριθμό
για κάποιον αρκετά μεγάλο πρώτο αριθμό 
 έχουμε
έχουμε  εκτός και αν ο
εκτός και αν ο  διαιρεί ακριβώς έναν από τους
διαιρεί ακριβώς έναν από τους  και δεν διαιρεί τον
και δεν διαιρεί τον  . Στην τελευταία περίπτωση, αν
. Στην τελευταία περίπτωση, αν  τότε έχουμε τα εξής:
τότε έχουμε τα εξής: 

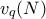 για την μεγαλύτερη δύναμη του
για την μεγαλύτερη δύναμη του  η οποία διαιρεί τον
η οποία διαιρεί τον  . Στην τρίτη γραμμή χρησιμοποιήσαμε το Lifting The Exponenent Lemma. (Ο
. Στην τρίτη γραμμή χρησιμοποιήσαμε το Lifting The Exponenent Lemma. (Ο  διαιρεί τον
διαιρεί τον 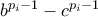 . Στην τέταρτη γραμμή χρησιμοποιήσαμε το γεγονός ότι ο
. Στην τέταρτη γραμμή χρησιμοποιήσαμε το γεγονός ότι ο  είναι αρκετά μεγάλος και ειδικότερα ότι είναι μεγαλύτερος του
είναι αρκετά μεγάλος και ειδικότερα ότι είναι μεγαλύτερος του  .
.  . Επίσης αν
. Επίσης αν  τότε θέτουμε
τότε θέτουμε  . Μπορούμε να υποθέσουμε ότι
. Μπορούμε να υποθέσουμε ότι  για κάθε
για κάθε  . Επομένως παίρνουμε
. Επομένως παίρνουμε
 είναι οι
είναι οι  καταλήγουμε στο ότι
καταλήγουμε στο ότι  Αυτό όμως είναι άτοπο για
Αυτό όμως είναι άτοπο για  αρκετά μεγάλο.
αρκετά μεγάλο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες