 ορίζεται με τις σχέσεις:
ορίζεται με τις σχέσεις: ,
, 
Να δείξετε ότι όλοι οι όροι της ακολουθίας είναι θετικοί ακέραιοι.
Συντονιστές: cretanman, silouan, rek2
 οπότε έχουμε τις σχέσεις
οπότε έχουμε τις σχέσεις


 ικανοποιεί την
ικανοποιεί την 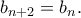 Επειδή προφανώς είναι
Επειδή προφανώς είναι  είναι
είναι .
. για κάθε
για κάθε 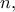 όπου
όπου  Τώρα το ζητούμενο είναι άμεσο επαγωγικά.
Τώρα το ζητούμενο είναι άμεσο επαγωγικά. είναι θετικοί ακέραιοι, τότε και ο
είναι θετικοί ακέραιοι, τότε και ο  είναι θετικός ακέραιος.
είναι θετικός ακέραιος.


 . Οπότε ο
. Οπότε ο  είναι ακέραιος, προφανώς θετικός.
είναι ακέραιος, προφανώς θετικός.  και
και  είναι θετικοί ακέραιοι.
είναι θετικοί ακέραιοι.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης