Να λυθεί στους φυσικούς η εξίσωση

Συντονιστές: cretanman, silouan, rek2

Δεν καταλαβαίνω. Αν θέλεις να βάλεις λύση μπορείς να το κάνεις εδώ. Εδώ προτάθηκε το θέμα, εδώ αναμένουμε τις λύσεις.nikhtas30 έγραψε: ↑Δευ Απρ 06, 2020 2:17 amΚαλησπέρα έκανα μια απόπειρα να λύσω το πρόβλημα σας και βρήκα μια λύση δεν είμαι σίγουρος αν υπαρχουν κι' άλλες.Η απόδειξη που έκανα είναι στο παρακάτω link:
https://m.facebook.com/groups/218401806 ... 4759473835


 , εφόσον
, εφόσον 
 , εφόσον
, εφόσον 


 , που ισχύει.
, που ισχύει.
Το γεγονός ότι υπάρχει global λύση για
 δεν μπορώ να καταλάβω πως μια λύση μόνο με κάποιο mod επιχείρημα μπορεί να προκύψει? Αναμένω τη λύση!
δεν μπορώ να καταλάβω πως μια λύση μόνο με κάποιο mod επιχείρημα μπορεί να προκύψει? Αναμένω τη λύση! αδυνατη για
αδυνατη για  παιρνωντας
παιρνωντας  και επειδη ο αριθμος πρεπει να τελειωνει σε 9 πρεπει το α να ειναι πολ του 3 αρα
και επειδη ο αριθμος πρεπει να τελειωνει σε 9 πρεπει το α να ειναι πολ του 3 αρα  .Τωρα η εξισωση γινεται
.Τωρα η εξισωση γινεται  αρα το
αρα το  .Κανωντας αντικατασταση βγαινει
.Κανωντας αντικατασταση βγαινει  επειδη
επειδη  πρεπει το 89 να διαιρει ενα απο τα δυο ομως το 89 ειναι πρωτος και δεν ισχυει αυτο.Αρα πρεπει b=1 και μετα με αντικατασταση ειναι
πρεπει το 89 να διαιρει ενα απο τα δυο ομως το 89 ειναι πρωτος και δεν ισχυει αυτο.Αρα πρεπει b=1 και μετα με αντικατασταση ειναι  .ΛΥσεις (χ,y)=(3,33),(3,-33)
.ΛΥσεις (χ,y)=(3,33),(3,-33)stamas1 έγραψε: ↑Τρί Απρ 07, 2020 1:21 pmΓιααδυνατη για
παιρνωντας
και επειδη ο αριθμος πρεπει να τελειωνει σε 9 πρεπει το α να ειναι πολ του 3 αρα
.Τωρα η εξισωση γινεται
αρα το
.Κανωντας αντικατασταση βγαινει
επειδη
πρεπει το 89 να διαιρει ενα απο τα δυο ομως το 89 ειναι πρωτος και δεν ισχυει αυτο.Αρα πρεπει b=1 και μετα με αντικατασταση ειναι
.ΛΥσεις (χ,y)=(3,33),(3,-33)
η σωστή είναι

Αν και δεν έχει σημασία μιας και δεν το έχουμε γιατί είναι άτοπο;
 .Ομως
.Ομως  αρα το 3 διαιρει το ενα και το 11 το αλλο.Αν το 3 διαρει την πρωτη παρενθεση τοτε το 11 διαρει την αλλη ομως αυτο ειναι ατοπο.Αν το 11 διαρει την πρωτη παρενθεση τοτε το 3 δεν διαιρει την δευτερη γιατι το αθροισμα των ψηφιων ειναι 2 αρα b=1 ....
αρα το 3 διαιρει το ενα και το 11 το αλλο.Αν το 3 διαρει την πρωτη παρενθεση τοτε το 11 διαρει την αλλη ομως αυτο ειναι ατοπο.Αν το 11 διαρει την πρωτη παρενθεση τοτε το 3 δεν διαιρει την δευτερη γιατι το αθροισμα των ψηφιων ειναι 2 αρα b=1 ....Αυτό δεν ισχύει. Για
 έχουμε ότι
έχουμε ότι  .
.Πως προσεγγίζεις τη λύση, με Pell εξισώσεις? Δεν έχω προλάβει να ασχοληθώ αλλά κάτι τέτοιο έχω στο μυαλό μου.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Απρ 07, 2020 5:06 pmΝομίζω ότι οι μοναδικές λύσεις είναι οικαι
.Αν δεν δοθεί λύση κάποια στιγμη θα γράψω την λύση.
 είναι άρτιος είναι εύκολο να δούμε ότι δεν υπάρχει λύση.
είναι άρτιος είναι εύκολο να δούμε ότι δεν υπάρχει λύση. (*)
(*) δεν υπάρχει λύση.
δεν υπάρχει λύση. έχουμε τις λύσεις
έχουμε τις λύσεις  και
και 
 δεν υπάρχουν λύσεις.
δεν υπάρχουν λύσεις. και
και  βρίσκουμε ότι
βρίσκουμε ότι 
 ώστε
ώστε  (1)
(1)
 (2)
(2)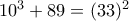 (3)
(3)
 φυσικός ώστε
φυσικός ώστε
 είναι περιττός .
είναι περιττός .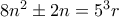
 )
) είναι άρτιος.
είναι άρτιος.Σταύρο, από την (1) βρίσκω ότι
 , την (2) δεν την βλέπω.
, την (2) δεν την βλέπω. να είναι περιττός και
να είναι περιττός και  .
.  και βρίσκω ότι (παίρνω υπόψη ότι
και βρίσκω ότι (παίρνω υπόψη ότι  περιττός)
περιττός) 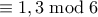 (απορρίπτεται δηλαδή το
(απορρίπτεται δηλαδή το  ).
). έχω
έχω  , επομένως
, επομένως  οπότε
οπότε  , άτοπο. Επομένως
, άτοπο. Επομένως  .
.  , που είναι εξίσωση τύπου Mordell. Ξέρουμε ότι αυτή έχει πεπερασμένες λύσεις και μάλιστα όλες οι θετικές λύσεις για το
, που είναι εξίσωση τύπου Mordell. Ξέρουμε ότι αυτή έχει πεπερασμένες λύσεις και μάλιστα όλες οι θετικές λύσεις για το  είναι
είναι  και
και  . Επειδή το
. Επειδή το  στην περίπτωσή μας είναι είναι δύναμη του 10, η μόνη δεκτή λύση είναι η
στην περίπτωσή μας είναι είναι δύναμη του 10, η μόνη δεκτή λύση είναι η  οπότε
οπότε  .
. Ωραία λύση!silouan έγραψε: ↑Τετ Απρ 08, 2020 6:35 pmΜια απόπειρα που δεν είναι στοιχειώδης όμως.
Όπως είδαμε πρέπει ονα είναι περιττός και
.
Παίρνω τώρακαι βρίσκω ότι (παίρνω υπόψη ότι
περιττός)
(απορρίπτεται δηλαδή το
).
Αν πάρω τώραέχω
, επομένως
οπότε
, άτοπο. Επομένως
.
Καταλήγουμε δηλαδή στην εξίσωση, που είναι εξίσωση τύπου Mordell. Ξέρουμε ότι αυτή έχει πεπερασμένες λύσεις και μάλιστα όλες οι θετικές λύσεις για το
είναι
και
. Επειδή το
στην περίπτωσή μας είναι είναι δύναμη του 10, η μόνη δεκτή λύση είναι η
οπότε
.
Για την εξίσωση Mordell δείτε εδώ https://hr.userweb.mwn.de/numb/mordell.html#tbl5
Θάνο φαντάζομαι ότι θα έχεις στο μυαλό σου μια πιο στοιχειώδη λύση από αυτή που πρότεινα παραπάνω, σωστά;
 άρτιο είναι τετριμμένο. Ας είναι λοιπόν
άρτιο είναι τετριμμένο. Ας είναι λοιπόν 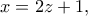 οπότε η εξίσωση γράφεται
οπότε η εξίσωση γράφεται , όπου
, όπου  , που είναι τύπου Pell.
, που είναι τύπου Pell.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες