 ώστε
ώστε  .
.Φιλικά,
Μάριος
Συντονιστές: cretanman, silouan, rek2
 ώστε
ώστε  .
. ή
ή  ή
ή 
 ανέβαινε κατά
ανέβαινε κατά  κάθε φορά.
κάθε φορά.  ή...ή
ή...ή  , τότε
, τότε  ή...ή
ή...ή  , τότε
, τότε  και ούτω καθεξής
και ούτω καθεξής και
και 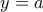 και
και  Αρκεί να βρω τρόπο να αποδείξω ότι
Αρκεί να βρω τρόπο να αποδείξω ότι  για κάθε
για κάθε  και
και 
Για
 άρτιο δεν έχουμε μεγάλο πρόβλημα.
άρτιο δεν έχουμε μεγάλο πρόβλημα. περιττό, θα μπορούσε να δουλέψει το εξής:
περιττό, θα μπορούσε να δουλέψει το εξής: που είναι μια γενικευμένη Pell με την οποία δεν έχω τις γνώσεις να ασχοληθώ.
που είναι μια γενικευμένη Pell με την οποία δεν έχω τις γνώσεις να ασχοληθώ.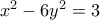 περιγράφεται εδώ: https://www.google.com/url?sa=t&source= ... 8598252147
περιγράφεται εδώ: https://www.google.com/url?sa=t&source= ... 8598252147 περιττό-τα άλλα εύκολα)-αν και εμπεριέχει λίγη "τύχη").
περιττό-τα άλλα εύκολα)-αν και εμπεριέχει λίγη "τύχη"). .
. .
.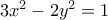 (1) και ελπίζουμε να περιορίσουμε κάπως τις δυνάμεις του
(1) και ελπίζουμε να περιορίσουμε κάπως τις δυνάμεις του  που αποτελούν λύσεις για το
που αποτελούν λύσεις για το  .
. .
. δίνεται από το ζεύγος
δίνεται από το ζεύγος  .
. .
. ;.
;. " της (1).
" της (1). ,στη γενική περίπτωση
,στη γενική περίπτωση  έχει τη μορφή
έχει τη μορφή  .
.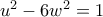 για την οποία βρίσκουμε την
για την οποία βρίσκουμε την  ως θεμελιώδη λύση.
ως θεμελιώδη λύση. είναι
είναι  για την
για την  και
και  .
. στην πρώτη και το
στην πρώτη και το  στη δεύτερη,για να πάρουμε τις σαφώς φιλικότερες
στη δεύτερη,για να πάρουμε τις σαφώς φιλικότερες  και
και 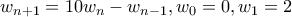 .Εδώ απλώς κοτσάραμε την
.Εδώ απλώς κοτσάραμε την  ως τετριμμένη λύση-που όμως περιέχεται στην ακολουθία.
ως τετριμμένη λύση-που όμως περιέχεται στην ακολουθία. έχουν τον ίδιο αναδρομικό τύπο.
έχουν τον ίδιο αναδρομικό τύπο. (γραμμικός συνδυασμός τους).
(γραμμικός συνδυασμός τους). .
. .
. την παραπάνω.
την παραπάνω. και μετά ξανά από την αρχή-αναμενόμενο να "ανακυκλώνονται" από Περιστεροφωλιά.
και μετά ξανά από την αρχή-αναμενόμενο να "ανακυκλώνονται" από Περιστεροφωλιά. διαιρεί όρο της ακολουθίας,τότε αυτή διαιρείται και από κάτι άλλο οπότε αποκλείεται κάποιος όρος να περιέχει μόνο τριάρια.
διαιρεί όρο της ακολουθίας,τότε αυτή διαιρείται και από κάτι άλλο οπότε αποκλείεται κάποιος όρος να περιέχει μόνο τριάρια. .
. την ακολουθία,για να δούμε τι πάει στραβά. (και το
την ακολουθία,για να δούμε τι πάει στραβά. (και το  δουλεύει εντελώς κατά τύχη).
δουλεύει εντελώς κατά τύχη). και ξανά από την αρχή.
και ξανά από την αρχή. η περίοδος είναι ίδια με του
η περίοδος είναι ίδια με του  και τα μηδενικά πέφτουν στα ίδια ακριβώς σημεία.
και τα μηδενικά πέφτουν στα ίδια ακριβώς σημεία. που υπάρχουν στην ακολουθία είναι
που υπάρχουν στην ακολουθία είναι  που δίνουν ως λύσεις τις
που δίνουν ως λύσεις τις 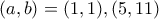 .
. τότε
τότε  .
. το οποίο είναι ευκλείδια περιοχή.
το οποίο είναι ευκλείδια περιοχή. .
. μπορούμε να πούμε ότι
μπορούμε να πούμε ότι  , το οποίο είναι ανάλυση σε πρώτους παράγοντες στο
, το οποίο είναι ανάλυση σε πρώτους παράγοντες στο  .
. είναι περιοχή μοναδικής παραγοντοποίησης έχουμε ότι:
είναι περιοχή μοναδικής παραγοντοποίησης έχουμε ότι: .
. δεν διαιρεί τον
δεν διαιρεί τον  στον
στον  .
. , το οποίο σημαίνει ότι
, το οποίο σημαίνει ότι  .
. . Οπότε
. Οπότε  και
και  .
. και το συμπέρασμα έπεται.
και το συμπέρασμα έπεται.Ωραία, καλή ανάλυση (την οποία υποθέτω έκανες για να με διευκολύνεις οπότε και σε ευχαριστώ). Δε μου ρθε καθόλου η νορμάλ Pell και βούτηξα στη γενικευμένη όπου την βρήκα κάπως λυμενη και το δεσα κόμπο ότι μόνο έτσι βγαίνει.min## έγραψε: ↑Παρ Αύγ 28, 2020 7:09 pmΕίναι ψιλοστάνταρ η διαδικασία (γιαπεριττό-τα άλλα εύκολα)-αν και εμπεριέχει λίγη "τύχη").
Για να τη δούμε:
Έστω.
Η δοθείσα γράφεται ως.
Μελετάμε λοιπόν τη διοφαντική(1) και ελπίζουμε να περιορίσουμε κάπως τις δυνάμεις του
που αποτελούν λύσεις για το
.
Βρίσκουμε αρχικά ως θεμελιώδη λύση την.
Από γνωστή θεωρία,η γενική λύσηδίνεται από το ζεύγος
.
Αυτό γράφεται απλούστερα ως.
Τι είναι τα;.
Είναι οι ακολουθίες των λύσεων της λεγόμενης "επιλύουσας" της (1).
Αυτή η,στη γενική περίπτωση
έχει τη μορφή
.
Οι σχετικές αποδείξεις των ισχυρισμών παραλείπονται-αν και δεν είναι ιδιαίτερα δύσκολες.
Στη συγκεκριμένη περίπτωση λοιπόν,η επιλύουσα για την (1) είναι ηγια την οποία βρίσκουμε την
ως θεμελιώδη λύση.
Ο γενικός αναδρομικός τύπος που προκύπτει από την παραπάνωείναι
για την
και
.
Απαλοίφουμε τοστην πρώτη και το
στη δεύτερη,για να πάρουμε τις σαφώς φιλικότερες
και
.Εδώ απλώς κοτσάραμε την
ως τετριμμένη λύση-που όμως περιέχεται στην ακολουθία.
Το σημαντικό είναι ότι οιέχουν τον ίδιο αναδρομικό τύπο.
Το ίδιο λοιπόν θα ισχύει και για τη(γραμμικός συνδυασμός τους).
Τσεκάροντας τις αρχικές συνθήκες παίρνουμε:
.
Η δυσκολία εδώ έγκειται στο ότι οι πρώτοι δύο όροι είναι ήδη δυνάμεις του.
Παίρνουμετην παραπάνω.
Βλέπουμε ότι τα υπόλοιπα που αφήνει είναι τα :και μετά ξανά από την αρχή-αναμενόμενο να "ανακυκλώνονται" από Περιστεροφωλιά.
Θα θέλαμε να δείξουμε ότι όποτε μια μεγάλη δύναμη τουδιαιρεί όρο της ακολουθίας,τότε αυτή διαιρείται και από κάτι άλλο οπότε αποκλείεται κάποιος όρος να περιέχει μόνο τριάρια.
Ας πάρουμε το αμέσως επόμενο μηδενικό.
Είναι.
Ας πάρουμε λοιπόντην ακολουθία,για να δούμε τι πάει στραβά. (και το
δουλεύει εντελώς κατά τύχη).
Τα υπόλοιπα που αφήνει είναι τα :και ξανά από την αρχή.
Εντελώς τυχαία (ή ίσως όχι),αν πάρουμεη περίοδος είναι ίδια με του
και τα μηδενικά πέφτουν στα ίδια ακριβώς σημεία.
Επομένως οι μόνες δυνάμεις τουπου υπάρχουν στην ακολουθία είναι
που δίνουν ως λύσεις τις
.
Συνεχίζοντας...stranger έγραψε: ↑Παρ Αύγ 28, 2020 7:19 pmΘα δείξω ότι αντότε
.
Δουλεύουμε στοτο οποίο είναι ευκλείδια περιοχή.
Μπορούμε να γράψουμε την αρχική ως εξής:.
Άρα επειδήμπορούμε να πούμε ότι
, το οποίο είναι ανάλυση σε πρώτους παράγοντες στο
.
Άρα αφού τοείναι περιοχή μοναδικής παραγοντοποίησης έχουμε ότι:
.
Όμως τοδεν διαιρεί τον
στον
.
Άρα, το οποίο σημαίνει ότι
.
Παίρνοντας απόλυτες τιμές έχουμε. Οπότε
και
.
Άρακαι το συμπέρασμα έπεται.
 και ότι ο
και ότι ο  είναι πραγματικός. Τότε παίρνοντας απόλυτες τιμές έχουμε
είναι πραγματικός. Τότε παίρνοντας απόλυτες τιμές έχουμε  .
. είναι ακέραιος όταν ο
είναι ακέραιος όταν ο  είναι φυσικός. Όπότε
είναι φυσικός. Όπότε  όπου
όπου  φυσικός αριθμός.
φυσικός αριθμός. . Άρα αφού ο
. Άρα αφού ο ![\mathbb{Z}[\sqrt{-2}] \mathbb{Z}[\sqrt{-2}]](/forum/ext/geomar/texintegr/latexrender/pictures/b408bc2cf2716f73c987afbc67186aac.png) είναι δακτύλιος έπεται ότι κάθε προσθαφαίρεση και πολλαπλασιασμός στοιχείων του είναι μέσα στον δακτύλιο. Άρα
είναι δακτύλιος έπεται ότι κάθε προσθαφαίρεση και πολλαπλασιασμός στοιχείων του είναι μέσα στον δακτύλιο. Άρα ![2 \sqrt{n} \in \mathbb{Z}[\sqrt{-2}] 2 \sqrt{n} \in \mathbb{Z}[\sqrt{-2}]](/forum/ext/geomar/texintegr/latexrender/pictures/565ef02e074a8893dd061b07da7e07a7.png) από το οποίο μπορούμε να βγάλουμε μετά ότι ο
από το οποίο μπορούμε να βγάλουμε μετά ότι ο  είναι τετράγωνο φυσικού. Άρα
είναι τετράγωνο φυσικού. Άρα  .
. .
.Έστω ότιnikhtas30 έγραψε: ↑Παρ Αύγ 28, 2020 8:46 amΚαλημέρα
Βρήκα εμπειρικά τις λύσεις
ή
ή
Βασικά καθόμουν και έκανα ανισώσεις (άσκοπες αριθμητικές πράξεις), αλλά στην ουσία είναι σαν να έκανα δοκιμές, αφού η τιμή τουανέβαινε κατά
κάθε φορά.
π.χ
ή...ή
, τότε
ή...ή
, τότε
και ούτω καθεξής
Έχω την αίσθηση ότι δεν υπάρχουν άλλες λύσεις και
δεν έχω τρόπο (εργαλεία) να αποδείξω ότι δεν υπάρχουν άλλες λύσεις. Οπότε τ'αφήνω έτσι για τώρα.
Edit γιακαι
και
Graph_2020-08-28_09-42-04.pngScreenshot_20200829-035050.png
Αρκεί να βρω τρόπο να αποδείξω ότιγια κάθε
και

 για κάθε
για κάθε  και
και 

 , Άτοπο, οπότε
, Άτοπο, οπότε  για κάθε
για κάθε  και
και 
 για κάθε
για κάθε  και
και 
 και
και 
 και όχι για κάθε
και όχι για κάθε  .
.  και
και  θα μπορούσε κάποιος να
θα μπορούσε κάποιος να  και
και  ή το ανάποδο, οπότε δεν ισχύει ο ισχυρισμός μου ή κάποιος παρόμοιος.
ή το ανάποδο, οπότε δεν ισχύει ο ισχυρισμός μου ή κάποιος παρόμοιος.Δεν είναι συλλογιστική αυτή. Υποθέτεις ότιnikhtas30 έγραψε: ↑Κυρ Αύγ 30, 2020 3:08 amΈστω ότιnikhtas30 έγραψε: ↑Παρ Αύγ 28, 2020 8:46 amΚαλημέρα
Βρήκα εμπειρικά τις λύσεις
ή
ή
Βασικά καθόμουν και έκανα ανισώσεις (άσκοπες αριθμητικές πράξεις), αλλά στην ουσία είναι σαν να έκανα δοκιμές, αφού η τιμή τουανέβαινε κατά
κάθε φορά.
π.χ
ή...ή
, τότε
ή...ή
, τότε
και ούτω καθεξής
Έχω την αίσθηση ότι δεν υπάρχουν άλλες λύσεις και
δεν έχω τρόπο (εργαλεία) να αποδείξω ότι δεν υπάρχουν άλλες λύσεις. Οπότε τ'αφήνω έτσι για τώρα.
Edit γιακαι
και
Graph_2020-08-28_09-42-04.pngScreenshot_20200829-035050.png
Αρκεί να βρω τρόπο να αποδείξω ότιγια κάθε
και

για κάθε
και
άρα
δηλαδή
, Άτοπο, οπότε
για κάθε
και
με άλλα λόγια απέδειξα ότι
για κάθε
και
Συνεπώς δεν έχει λύσεις γιακαι
Άρα δεν χάνω λύσει άρα τελείωσα
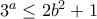 και καταλήγεις ότι
και καταλήγεις ότι  . Επίσης και το υπόλοιπο του κειμένου είναι γεμάτο λάθη.
. Επίσης και το υπόλοιπο του κειμένου είναι γεμάτο λάθη.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες