Βάζω μια λύση σε αυτήν την εξαιρετικά δύσκολη κατά την γνώμη μου άσκηση.
Η απάντηση είναι ότι κερδίζει ο Αντρέας.
Λήμμα 1: Έστω φυσικοί αριθμοί

, έστω ότι έχουμε γραμμένους στον πίνακα τους αριθμούς

, και έστω

μη αρνητικοί ακέραιοι. Τότε ο Αντρέας μπορεί να επιτύχει ένα από τα πιο κάτω
(α) Να αυξήσει τον

κατά

.
(β) Να μειώσει τον

κατά

.
(γ) Να κάνει τουλάχιστον

από τους

πολλαπλάσια του

.
Ας παρατηρήσουμε ότι το Λήμμα 1 είναι αρκετό για να δείξουμε ότι ο Ανδρέας κερδίζει το παιγνίδι. Αν

, παίρνουμε

οπότε από το Λήμμα 1 είτε κάνουμε τον

πολλαπλάσιο του

, είτε κάνουμε τουλάχιστον
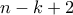
από τους υπόλοιπους πολλαπλάσια του

. Στην δεύτερη περίπτωση ο Ανδρέας κερδίζει άμεσα. Στην πρώτη περίπτωση κερδίζει επαναλαμβάνοντας την διαδικασία επαγωγικά.
Η απόδειξη του Λήμματος 1 θα είναι με επαγωγή στο

. Αν

και

είναι άμεσο αφού

ή

και δεν έχουμε κάτι να δείξουμε. Για

είναι επίσης άμεσο αφού αν

και

τότε

και επιλέγοντας τον

μπορούμε να πετύχουμε είτε το (α) είτε το (β).
Έστω λοιπόν ότι ο ισχυρισμός ισχύει για κάθε

με

. Θα δείξω ότι ισχύει και για κάθε

με

. Έστω λοιπόν ότι

Από την επαγωγική υπόθεση ο Αντρέας μπορεί να επιτύχει ένα από τα πιο κάτω:
(α) Να αυξήσει τον

κατά

.
(β) Να μειώσει τον

κατά

.
(γ) Να κάνει τουλάχιστον

από τους

πολλαπλάσια του

.
Προσοχή στο ότι μπορεί να πετύχει ένα από τα πιο πάνω χωρίς να πειράξει καθόλου τον

.
Αν πετύχει το (β) ή (γ) τελειώσαμε. Οπότε μπορούμε να υποθέσουμε ότι πέτυχε το (α). Τώρα μπορεί να επιλέξει όλους τους αριθμούς

. Αν αυξηθούν όλοι κατά

, τότε ο

αυξήθηκε συνολικά κατά

και τελειώσαμε. Μπορούμε λοιπόν να υποθέσουμε ότι όλοι μειώθηκαν κατά

και πιο συγκεκριμένα μειώσαμε τον

κατά

.
Έστω ότι με αυτήν την διαδικασία ο

έγινε τώρα

. (Ασφαλώς είναι

.) Από την επαγωγική υπόθεση ο Αντρέας μπορεί να επιτύχει ένα από τα πιο κάτω:
(α) Να αυξήσει τον

κατά

.
(β) Να μειώσει τον

κατά

.
(γ) Να κάνει τουλάχιστον

από τους

πολλαπλάσια του

.
Αν πετύχει τα (β),(γ) τότε τελειώσαμε ενώ αν πετύχει το (α) τότε στο επόμενο βήμα μπορεί να μειώσει τον

κατά

.
Επαναλαμβάνοντας την διαδικασία όσες φορές χρειαστεί ο Αντρέας θα καταφέρει είτε να αυξήσει συνολικά τον

κατά

, είτε να τον μειώσει κατά

είτε να κάνει τουλάχιστον

από τους

πολλαπλάσια του

είτε να κάνει τον

πολλαπλάσιο του

. Στις πρώτες τρεις περιπτώσεις το ζητούμενο αποδείχθηκε. Στην τελευταία περίπτωση το ζητούμενο έπεται επαγωγικά.
 με
με 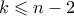 .
.  ακέραιοι αριθμοί. Σε κάθε βήμα ο Ανδρέας διαλέγει κάποιους συνεχόμενους αριθμούς (από
ακέραιοι αριθμοί. Σε κάθε βήμα ο Ανδρέας διαλέγει κάποιους συνεχόμενους αριθμούς (από  μέχρι
μέχρι  ) και ο Βασίλης επιλέγει είτε να προσθέσει σε όλους
) και ο Βασίλης επιλέγει είτε να προσθέσει σε όλους  είτε να αφαιρέσει από όλους
είτε να αφαιρέσει από όλους  .
. 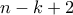 από αυτούς τους αριθμούς (ταυτοχρόνως) πολλαπλάσια του
από αυτούς τους αριθμούς (ταυτοχρόνως) πολλαπλάσια του  ενώ σκοπός του Βασίλη είναι να τον αποτρέψει.
ενώ σκοπός του Βασίλη είναι να τον αποτρέψει.
 , έστω ότι έχουμε γραμμένους στον πίνακα τους αριθμούς
, έστω ότι έχουμε γραμμένους στον πίνακα τους αριθμούς  , και έστω
, και έστω  μη αρνητικοί ακέραιοι. Τότε ο Αντρέας μπορεί να επιτύχει ένα από τα πιο κάτω
μη αρνητικοί ακέραιοι. Τότε ο Αντρέας μπορεί να επιτύχει ένα από τα πιο κάτω κατά
κατά  .
. .
. από τους
από τους  πολλαπλάσια του
πολλαπλάσια του  .
.  , παίρνουμε
, παίρνουμε  οπότε από το Λήμμα 1 είτε κάνουμε τον
οπότε από το Λήμμα 1 είτε κάνουμε τον  . Αν
. Αν  και
και  είναι άμεσο αφού
είναι άμεσο αφού  ή
ή  και δεν έχουμε κάτι να δείξουμε. Για
και δεν έχουμε κάτι να δείξουμε. Για  είναι επίσης άμεσο αφού αν
είναι επίσης άμεσο αφού αν  και
και  τότε
τότε  και επιλέγοντας τον
και επιλέγοντας τον  . Θα δείξω ότι ισχύει και για κάθε
. Θα δείξω ότι ισχύει και για κάθε  . Έστω λοιπόν ότι
. Έστω λοιπόν ότι  κατά
κατά  .
. πολλαπλάσια του
πολλαπλάσια του  .
.  . (Ασφαλώς είναι
. (Ασφαλώς είναι  .) Από την επαγωγική υπόθεση ο Αντρέας μπορεί να επιτύχει ένα από τα πιο κάτω:
.) Από την επαγωγική υπόθεση ο Αντρέας μπορεί να επιτύχει ένα από τα πιο κάτω: .
. .
.