 , όπου
, όπου  πραγματική παράμετρος.
πραγματική παράμετρος.Να βρεθεί ο
 ώστε οι ρίζες της
ώστε οι ρίζες της  , να επαληθεύουν τη σχέση
, να επαληθεύουν τη σχέση  .
.Συντονιστής: stranton
 , όπου
, όπου  πραγματική παράμετρος.
πραγματική παράμετρος. ώστε οι ρίζες της
ώστε οι ρίζες της  , να επαληθεύουν τη σχέση
, να επαληθεύουν τη σχέση  .
.Πρέπειgiorgos milonakos έγραψε: ↑Τετ Μάιος 23, 2018 6:23 pmΔίνεται η εξίσωση, όπου
πραγματική παράμετρος.
Να βρεθεί οώστε οι ρίζες της
, να επαληθεύουν τη σχέση
.
![\Delta \geq 0\Leftrightarrow (a-2)^2-4(a^2+1)\geq 0\Leftrightarrow a\in[-\frac{4}{3},0]. \Delta \geq 0\Leftrightarrow (a-2)^2-4(a^2+1)\geq 0\Leftrightarrow a\in[-\frac{4}{3},0].](/forum/ext/geomar/texintegr/latexrender/pictures/747227f8ba0ac347b00e817dab71f688.png)



![\Leftarrow a\in[-\frac{4}{3},0]\cap \left ( (-\infty ,-1)\cup (5,+\infty ) \right )=[-\frac{4}{3},-1). \Leftarrow a\in[-\frac{4}{3},0]\cap \left ( (-\infty ,-1)\cup (5,+\infty ) \right )=[-\frac{4}{3},-1).](/forum/ext/geomar/texintegr/latexrender/pictures/7f0a6b9a51f8dcb33672631cb9269f42.png)

 ή
ή 
Ας λυθεί και όταν οι ρίζες είναι μιγαδικές,οπότε οι απόλυτες τιμές γίνονται μέτρα.giorgos milonakos έγραψε: ↑Τετ Μάιος 23, 2018 6:23 pmΔίνεται η εξίσωση, όπου
πραγματική παράμετρος.
Να βρεθεί οώστε οι ρίζες της
, να επαληθεύουν τη σχέση
.
ΠρέπειΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Νοέμ 10, 1970 5:45 pmΑς λυθεί και όταν οι ρίζες είναι μιγαδικές,οπότε οι απόλυτες τιμές γίνονται μέτρα.giorgos milonakos έγραψε: ↑Τετ Μάιος 23, 2018 6:23 pmΔίνεται η εξίσωση, όπου
πραγματική παράμετρος.
Να βρεθεί οώστε οι ρίζες της
, να επαληθεύουν τη σχέση
.
Εκτός φακέλου φυσικά αλλά εντός Μαθηματικής περιέργειας.

 με κοινό μέτρο
με κοινό μέτρο 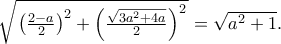

 παίρνουμε
παίρνουμε 
Τελικά αν δεν υποθέσουμε ότι οι ρίζες είναι πραγματικές η απάντηση είναιgiorgos milonakos έγραψε: ↑Τετ Μάιος 23, 2018 6:23 pmΔίνεται η εξίσωση, όπου
πραγματική παράμετρος.
Να βρεθεί οώστε οι ρίζες της
, να επαληθεύουν τη σχέση
.

Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot], KARKAR και 6 επισκέπτες