 ισχύει
ισχύει  , να αποδείξετε ότι η εξίσωση:
, να αποδείξετε ότι η εξίσωση:  έχει δύο ρίζες άνισες.
έχει δύο ρίζες άνισες.Συντονιστής: stranton
 ισχύει
ισχύει  , να αποδείξετε ότι η εξίσωση:
, να αποδείξετε ότι η εξίσωση:  έχει δύο ρίζες άνισες.
έχει δύο ρίζες άνισες. )
) . Τότε
. Τότε  . Άρα
. Άρα  . (1) . Και διακρίνουμε τις εξής υποπεριπτώσεις:
. (1) . Και διακρίνουμε τις εξής υποπεριπτώσεις: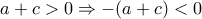 και άρα θα είναι και
και άρα θα είναι και 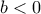 . Τότε από την (1) έχουμε:
. Τότε από την (1) έχουμε:
 . Τότε
. Τότε  . Άρα
. Άρα  . Άρα
. Άρα  και έχουμε και πάλι το ζητούμενο.
και έχουμε και πάλι το ζητούμενο. Τότε
Τότε  . Θα διακρίνουμε και πάλι δύο υποπεριπτώσεις:
. Θα διακρίνουμε και πάλι δύο υποπεριπτώσεις: . Τότε
. Τότε  . Άρα
. Άρα  και συνεπώς
και συνεπώς  , άρα το ζητούμενο
, άρα το ζητούμενο . Τότε αφού είναι και
. Τότε αφού είναι και  , θα έχουμε
, θα έχουμε  και από
και από 
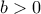 . Άρα από την σχέση
. Άρα από την σχέση  παίρνουμε
παίρνουμε  και όπως είδαμε και πιο πάνω θα είναι
και όπως είδαμε και πιο πάνω θα είναι  , και η απόδειξη ολοκληρώθηκε.
, και η απόδειξη ολοκληρώθηκε.Οπως έγραψε ο Δημήτρης πρέπει

 (1)
(1) έχει δύο άνισες ρίζες.
έχει δύο άνισες ρίζες.

 .
. .
. που είναι διαφορετικές.
που είναι διαφορετικές.  και
και 


 και
και 
Μία ρίζα είναι σίγουρη αφού
 . Αν οι ρίζες ήταν ίσες, τότε θα ίσχυε
. Αν οι ρίζες ήταν ίσες, τότε θα ίσχυε  . Αλλά τότε από την υπόθεση θα είχαμε
. Αλλά τότε από την υπόθεση θα είχαμε , άτοπο.
, άτοπο. .
. να βρίσκεται στο πάνω ημιεπίπεδο ολόκληρη η στο κάτω ημιεπίπεδο ολόκληρη επειδή
να βρίσκεται στο πάνω ημιεπίπεδο ολόκληρη η στο κάτω ημιεπίπεδο ολόκληρη επειδή  , το οποίο είναι άτοπο αφού
, το οποίο είναι άτοπο αφού  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες