ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Σάβ Αύγ 28, 2021 9:44 pm
Πριν λίγες μέρες βρήκα ένα κιτρινισμένο χαρτί στο οποίο είχα γράψει τη λύση ενός θέματος πριν κάποιες δεκαετίες...
Δυστυχώς δεν είχα γράψει την προέλευση του θέματος. Πρόκειται για ένα θέμα με τριώνυμο, κλασσικό πριν 50 και πλέον χρόνια ωστόσο παραμένει ενδιαφέρον και σήμερα μολονότι δεν έχει πλέον θέση στη σχολική διδασκαλία. Το μοιράζομαι μαζί σας για να το δουν και οι μαθητές που παρακολουθούν το mathematica.
Για ποιες τιμές του

το
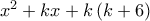
είναι αρνητικό για κάθε

;
Αν το τριώνυμό μας έχει ρίζα στο διάστημα
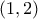
, έστω την

, τότε είτε για
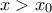
, είτε για

θα είναι μη αρνητικό. Άρα δεν θα πρέπει να έχει ρίζες στο διάστημα

. Εφόσον θέλουμε να έχει αρνητικές τιμές σε αυτό και ο συντελεστής του μεγιστοβάθμιου όρου είναι θετικός, η διακρίνουσά του θα πρέπει να είναι θετική. Άρα θα έχει πρέπει να έχει δυο ρίζες.
Αν και οι δυο ρίζες είναι είτε μεγαλύτερες ή ίσες του

, είτε μικρότερες ή ίσες του

τότε για κάποια

, μικρότερα του

το τριώνυμο θα είναι θετικό και αντίστοιχα για κάποια

μεγαλύτερα του

το τριώνυμο θα είναι θετικό.
Επομένως για να ικονοποιείται το ζητούμενο θα πρέπει το τριώνυμό μας να έχει ακριβώς μια ρίζα στο διάστημα
![(-\infty, 1] (-\infty, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/b954873d2ca8398fbba095c891dbf31a.png)
και ακριβώς μια ρίζα στο διάστημα

.
Στο σημείο αυτό θα χρησιμοποιήσουμε τις παρακάτω προτάσεις για τριώνυμο της γενικής μορφής

, με τετμημένη της κορυφής της παραβολής

και διακρίνουσα

:
I Το τριώνυμο έχει ακριβώς μια ρίζα στο
![(-\infty, M] \Leftrightarrow a \cdot f(M) < 0 (-\infty, M] \Leftrightarrow a \cdot f(M) < 0](/forum/ext/geomar/texintegr/latexrender/pictures/75f798136a7a78eedf0dcc7d4be10a7d.png)
ή
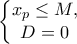
ή
 II
II Το τριώνυμο έχει ακριβώς μια ρίζα στο

ή

ή
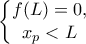
Παραλείπω προς το παρόν τις αποδείξεις των παραπάνω προτάσεων και απλά θα τις εφαρμόσουμε.
Άρα στην περίπτωσή μας θα είναι τα

(από την πρώτη πρόταση) για τα οποία

σε ένωση με το σύνολο των

που προκύπτει από σύστημα

και
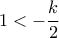
. Το τελευταίο έχει λύση μόνο τον αριθμό

καθόσον

δεν είναι μεγαλύτερο του

. Άρα τα

που ικανοποιούν την πρώτη πρόταση είναι

Ομοίως από την δεύτερη πρόταση θα έχουμε τα

για τα οποία

σε ένωση με το σύνολο των

που προκύπτει από σύστημα

και

. Το τελευταίο έχει λύση μόνο τον αριθμό

καθόσον ο αριθμός

δεν είναι μικρότερος του

. Άρα τα

που ικανοποιούν την δεύτερη πρόταση είναι
![k \in \left ( -4-2\sqrt{3}, -4+2\sqrt{3} \right ] k \in \left ( -4-2\sqrt{3}, -4+2\sqrt{3} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/7c5cd0d37a3294a6c55fa60501ef3ca3.png)
.
Εν τέλη τα ζητούμενα

ανήκουν στο σύνολο
![\left [ \dfrac{-7-3\sqrt{5}}{2}, \dfrac{-7+3\sqrt{5}}{2} \right ) \cap \left ( -4-2\sqrt{3}, -4+2\sqrt{3} \right ] = \left [ \dfrac{-7-3\sqrt{5}}{2}, -4+2\sqrt{3} \right ] \left [ \dfrac{-7-3\sqrt{5}}{2}, \dfrac{-7+3\sqrt{5}}{2} \right ) \cap \left ( -4-2\sqrt{3}, -4+2\sqrt{3} \right ] = \left [ \dfrac{-7-3\sqrt{5}}{2}, -4+2\sqrt{3} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/9df9f9f86139a4811f475e8932dc8b40.png)
εφόσον

επειδή (

)
και

. επειδή
 Edit: Έγινε διόρθωση στη σύγκριση των άκρων των διαστημάτων έπειτα από παρατήρηση του θεματοδότη.
Edit: Έγινε διόρθωση στη σύγκριση των άκρων των διαστημάτων έπειτα από παρατήρηση του θεματοδότη. το
το 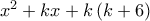 είναι αρνητικό για κάθε
είναι αρνητικό για κάθε  ;
;
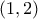 , έστω την
, έστω την  , τότε είτε για
, τότε είτε για 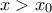 , είτε για
, είτε για  θα είναι μη αρνητικό. Άρα δεν θα πρέπει να έχει ρίζες στο διάστημα
θα είναι μη αρνητικό. Άρα δεν θα πρέπει να έχει ρίζες στο διάστημα  . Εφόσον θέλουμε να έχει αρνητικές τιμές σε αυτό και ο συντελεστής του μεγιστοβάθμιου όρου είναι θετικός, η διακρίνουσά του θα πρέπει να είναι θετική. Άρα θα έχει πρέπει να έχει δυο ρίζες.
. Εφόσον θέλουμε να έχει αρνητικές τιμές σε αυτό και ο συντελεστής του μεγιστοβάθμιου όρου είναι θετικός, η διακρίνουσά του θα πρέπει να είναι θετική. Άρα θα έχει πρέπει να έχει δυο ρίζες. , είτε μικρότερες ή ίσες του
, είτε μικρότερες ή ίσες του  τότε για κάποια
τότε για κάποια  , μικρότερα του
, μικρότερα του ![(-\infty, 1] (-\infty, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/b954873d2ca8398fbba095c891dbf31a.png) και ακριβώς μια ρίζα στο διάστημα
και ακριβώς μια ρίζα στο διάστημα  .
. , με τετμημένη της κορυφής της παραβολής
, με τετμημένη της κορυφής της παραβολής  και διακρίνουσα
και διακρίνουσα  :
:![(-\infty, M] \Leftrightarrow a \cdot f(M) < 0 (-\infty, M] \Leftrightarrow a \cdot f(M) < 0](/forum/ext/geomar/texintegr/latexrender/pictures/75f798136a7a78eedf0dcc7d4be10a7d.png) ή
ή 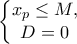 ή
ή 
 ή
ή  ή
ή 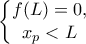
 σε ένωση με το σύνολο των
σε ένωση με το σύνολο των  και
και 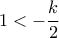 . Το τελευταίο έχει λύση μόνο τον αριθμό
. Το τελευταίο έχει λύση μόνο τον αριθμό  καθόσον
καθόσον  δεν είναι μεγαλύτερο του
δεν είναι μεγαλύτερο του 
 σε ένωση με το σύνολο των
σε ένωση με το σύνολο των  και
και  . Το τελευταίο έχει λύση μόνο τον αριθμό
. Το τελευταίο έχει λύση μόνο τον αριθμό  καθόσον ο αριθμός
καθόσον ο αριθμός  δεν είναι μικρότερος του
δεν είναι μικρότερος του ![k \in \left ( -4-2\sqrt{3}, -4+2\sqrt{3} \right ] k \in \left ( -4-2\sqrt{3}, -4+2\sqrt{3} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/7c5cd0d37a3294a6c55fa60501ef3ca3.png) .
.![\left [ \dfrac{-7-3\sqrt{5}}{2}, \dfrac{-7+3\sqrt{5}}{2} \right ) \cap \left ( -4-2\sqrt{3}, -4+2\sqrt{3} \right ] = \left [ \dfrac{-7-3\sqrt{5}}{2}, -4+2\sqrt{3} \right ] \left [ \dfrac{-7-3\sqrt{5}}{2}, \dfrac{-7+3\sqrt{5}}{2} \right ) \cap \left ( -4-2\sqrt{3}, -4+2\sqrt{3} \right ] = \left [ \dfrac{-7-3\sqrt{5}}{2}, -4+2\sqrt{3} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/9df9f9f86139a4811f475e8932dc8b40.png)
 επειδή (
επειδή ( )
) . επειδή
. επειδή
 του διαστήματος. Η δεύτερη αντιστοιχεί στο άκρο του διαστήματος
του διαστήματος. Η δεύτερη αντιστοιχεί στο άκρο του διαστήματος