
Υ.Γ Θα την αφήσω όσο θέλετε και μετά θα παραθέσω τη λύση μου. Όσοι φοιτητές είστε εδώ, προσπαθήστε το αν θέλετε
Συντονιστής: Demetres

.

 επειδή ισχύει
επειδή ισχύει  , ισοδύναμα
, ισοδύναμα  , έχουμε
, έχουμε  . Άρα
. Άρα ![\displaystyle{ I_2= \int_{0}^{1}\left ( \int_{x}^{1}\left ( \frac{x}{y} \right )^{2}dy\right ) dx = \int_{0}^{1}\left [ -\frac{x^2}{y} \right ]_{y=x}^{y=1} dx = \int_{0}^{1}(-x^2 + x) = \dfrac {1}{6}} \displaystyle{ I_2= \int_{0}^{1}\left ( \int_{x}^{1}\left ( \frac{x}{y} \right )^{2}dy\right ) dx = \int_{0}^{1}\left [ -\frac{x^2}{y} \right ]_{y=x}^{y=1} dx = \int_{0}^{1}(-x^2 + x) = \dfrac {1}{6}}](/forum/ext/geomar/texintegr/latexrender/pictures/b05598175314b8ebe164d2529d1554c4.png)
 κάνουμε (για κάθε σταθερό
κάνουμε (για κάθε σταθερό  ) την αλλαγή μεταβλητής
) την αλλαγή μεταβλητής  . Είναι τότε
. Είναι τότε 
![\displaystyle{ \int_{0}^{1}\left (\dfrac {1}{t} - \left [\dfrac{1}{t} \right ] \right ) ^{2}dt = \sum _{n= 1}^{\infty } \int_{1/(n+1)}^{1/n}\left (\dfrac {1}{t^2} -\dfrac {2}{t}\left [\dfrac{1}{t} \right ] + \left [\dfrac{1}{t} \right ]^2 \right ) dt = \sum _{n= 1}^{\infty } \int_{1/(n+1)}^{1/n}\left (\dfrac {1}{t^2} -\dfrac {2n}{t} + n^2 \right ) dt= } \displaystyle{ \int_{0}^{1}\left (\dfrac {1}{t} - \left [\dfrac{1}{t} \right ] \right ) ^{2}dt = \sum _{n= 1}^{\infty } \int_{1/(n+1)}^{1/n}\left (\dfrac {1}{t^2} -\dfrac {2}{t}\left [\dfrac{1}{t} \right ] + \left [\dfrac{1}{t} \right ]^2 \right ) dt = \sum _{n= 1}^{\infty } \int_{1/(n+1)}^{1/n}\left (\dfrac {1}{t^2} -\dfrac {2n}{t} + n^2 \right ) dt= }](/forum/ext/geomar/texintegr/latexrender/pictures/c16025e169b3ee7abb472d1a29513328.png)
![\displaystyle{ = \sum _{n= 1}^{\infty } \left [ -\dfrac {1}{t} - 2n \ln t + n^2t \right ]_{1/(n+1)}^{1/n} = \sum _{n= 1}^{\infty } \left (1 +2n\ln \dfrac {n}{n+1} + 1-\dfrac {1}{n+1}\right ) \displaystyle{ = \sum _{n= 1}^{\infty } \left [ -\dfrac {1}{t} - 2n \ln t + n^2t \right ]_{1/(n+1)}^{1/n} = \sum _{n= 1}^{\infty } \left (1 +2n\ln \dfrac {n}{n+1} + 1-\dfrac {1}{n+1}\right )](/forum/ext/geomar/texintegr/latexrender/pictures/6df6ddb2802d07a1a70d6538d48be428.png)
 όρων της σειράς αυτής με χρήση του τύπου του Stirling δίνει
όρων της σειράς αυτής με χρήση του τύπου του Stirling δίνει 



 και
και  (αλλάζουν τα χωρία ολοκλήρωσης) και η Ιακωβιανή ορίζουσα είναι
(αλλάζουν τα χωρία ολοκλήρωσης) και η Ιακωβιανή ορίζουσα είναι  Επομένως :
Επομένως :








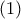 και
και  παίρνουμε:
παίρνουμε:
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης