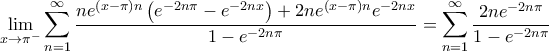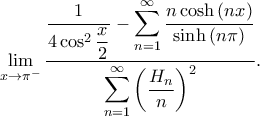
Όμορφο όριο που χρειάζεται χρόνο
Συντονιστής: Demetres
- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Όμορφο όριο που χρειάζεται χρόνο
Ας ξεκινήσουμε με το άθροισμα Au Yeung που είναι γνωστό.
Θα δείξουμε ότι
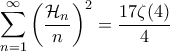 . Ως προς αυτό, ξεκινάμε με τη βασική σχέση
. Ως προς αυτό, ξεκινάμε με τη βασική σχέση 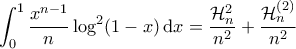
Από τη συμμετρία των αθροισμάτων Euler είναι
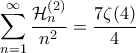
Τέλος,
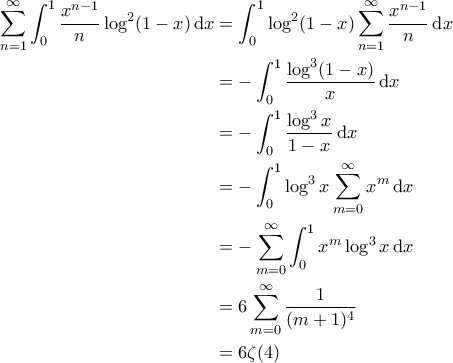
Η φαντασία είναι σημαντικότερη από τη γνώση !


Re: Όμορφο όριο που χρειάζεται χρόνο
Ωραία.  Προσωπικά, αυτό το άθροισμα το υπολόγισα έτσι:
Προσωπικά, αυτό το άθροισμα το υπολόγισα έτσι:
Θέτω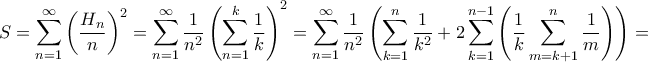
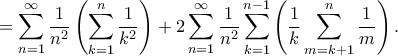
Θέτω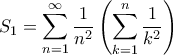 και
και 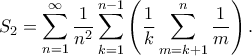
Είναι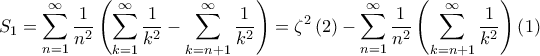
Αφού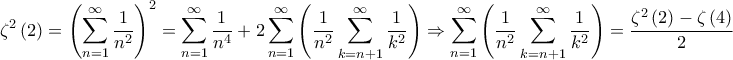
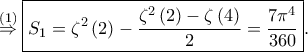
Επίσης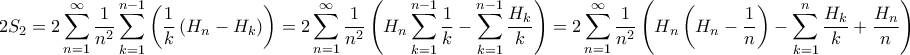
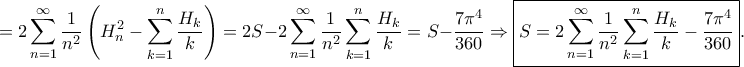
![\displaystyle H_{n}=\sum_{k=1}^{n}\frac{1}{k}=\sum_{k=1}^{n}\left ( \int\limits_{0}^{1}x^{k-1}dx \right )=\int\limits_{0}^{1}\frac{1-x^{n}}{1-x}dx=-\left [ \left ( 1-x^{n} \right )\ln \left ( 1-x \right ) \right ]_{0}^{1}-n\int\limits_{0}^{1}x^{n-1}\ln \left ( 1-x \right )dx \displaystyle H_{n}=\sum_{k=1}^{n}\frac{1}{k}=\sum_{k=1}^{n}\left ( \int\limits_{0}^{1}x^{k-1}dx \right )=\int\limits_{0}^{1}\frac{1-x^{n}}{1-x}dx=-\left [ \left ( 1-x^{n} \right )\ln \left ( 1-x \right ) \right ]_{0}^{1}-n\int\limits_{0}^{1}x^{n-1}\ln \left ( 1-x \right )dx](/forum/ext/geomar/texintegr/latexrender/pictures/c11d2b486788d7c8ead3d7bca5c053f3.png)
από όπου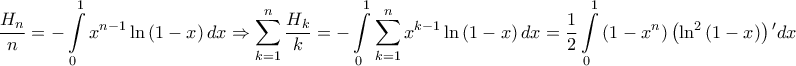
![\displaystyle =\frac{1}{2}\left [\left ( 1-x^{n} \right )\left ( \ln^{2}\left ( 1-x \right ) \right ) \right ]_{0}^{1}+\frac{n}{2}\int\limits_{0}^{1}x^{n-1}\left ( \ln^{2}\left ( 1-x \right ) \right )dx\Rightarrow \boxed{S=\sum_{n=1}^{\infty}\frac{1}{n}\int\limits_{0}^{1}x^{n-1}\left ( \ln^{2}\left ( 1-x \right ) \right )dx-\frac{7\pi ^{4}}{360}}. \displaystyle =\frac{1}{2}\left [\left ( 1-x^{n} \right )\left ( \ln^{2}\left ( 1-x \right ) \right ) \right ]_{0}^{1}+\frac{n}{2}\int\limits_{0}^{1}x^{n-1}\left ( \ln^{2}\left ( 1-x \right ) \right )dx\Rightarrow \boxed{S=\sum_{n=1}^{\infty}\frac{1}{n}\int\limits_{0}^{1}x^{n-1}\left ( \ln^{2}\left ( 1-x \right ) \right )dx-\frac{7\pi ^{4}}{360}}.](/forum/ext/geomar/texintegr/latexrender/pictures/dc597a76d3926337bc447a82c866f429.png)
Είναι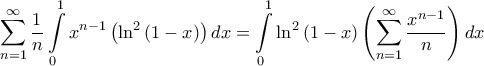
και από την σχέση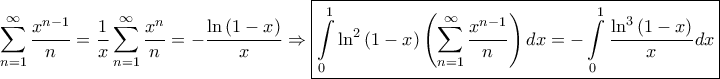
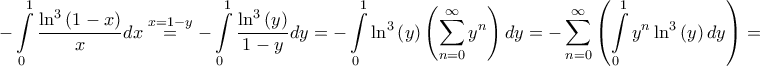
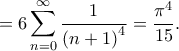
Τελικά λοιπόν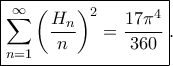
Υ.Γ Θα παραθέσω την αναλυτική λύση μου για το όριο, απλά την αφήνω λίγο στα χέρια των λυτών.
Θέτω
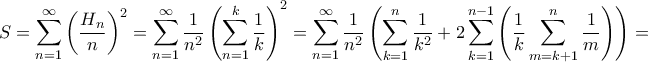
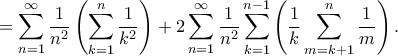
Θέτω
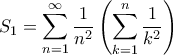 και
και 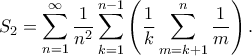
Είναι
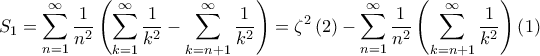
Αφού
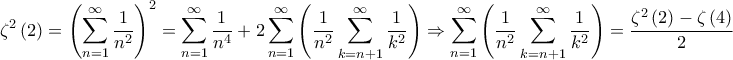
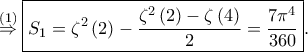
Επίσης
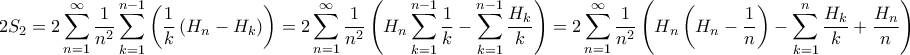
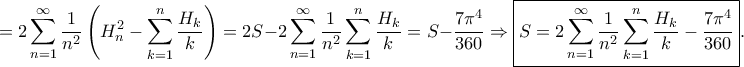
![\displaystyle H_{n}=\sum_{k=1}^{n}\frac{1}{k}=\sum_{k=1}^{n}\left ( \int\limits_{0}^{1}x^{k-1}dx \right )=\int\limits_{0}^{1}\frac{1-x^{n}}{1-x}dx=-\left [ \left ( 1-x^{n} \right )\ln \left ( 1-x \right ) \right ]_{0}^{1}-n\int\limits_{0}^{1}x^{n-1}\ln \left ( 1-x \right )dx \displaystyle H_{n}=\sum_{k=1}^{n}\frac{1}{k}=\sum_{k=1}^{n}\left ( \int\limits_{0}^{1}x^{k-1}dx \right )=\int\limits_{0}^{1}\frac{1-x^{n}}{1-x}dx=-\left [ \left ( 1-x^{n} \right )\ln \left ( 1-x \right ) \right ]_{0}^{1}-n\int\limits_{0}^{1}x^{n-1}\ln \left ( 1-x \right )dx](/forum/ext/geomar/texintegr/latexrender/pictures/c11d2b486788d7c8ead3d7bca5c053f3.png)
από όπου
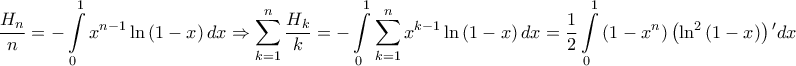
![\displaystyle =\frac{1}{2}\left [\left ( 1-x^{n} \right )\left ( \ln^{2}\left ( 1-x \right ) \right ) \right ]_{0}^{1}+\frac{n}{2}\int\limits_{0}^{1}x^{n-1}\left ( \ln^{2}\left ( 1-x \right ) \right )dx\Rightarrow \boxed{S=\sum_{n=1}^{\infty}\frac{1}{n}\int\limits_{0}^{1}x^{n-1}\left ( \ln^{2}\left ( 1-x \right ) \right )dx-\frac{7\pi ^{4}}{360}}. \displaystyle =\frac{1}{2}\left [\left ( 1-x^{n} \right )\left ( \ln^{2}\left ( 1-x \right ) \right ) \right ]_{0}^{1}+\frac{n}{2}\int\limits_{0}^{1}x^{n-1}\left ( \ln^{2}\left ( 1-x \right ) \right )dx\Rightarrow \boxed{S=\sum_{n=1}^{\infty}\frac{1}{n}\int\limits_{0}^{1}x^{n-1}\left ( \ln^{2}\left ( 1-x \right ) \right )dx-\frac{7\pi ^{4}}{360}}.](/forum/ext/geomar/texintegr/latexrender/pictures/dc597a76d3926337bc447a82c866f429.png)
Είναι
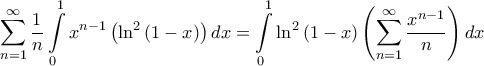
και από την σχέση
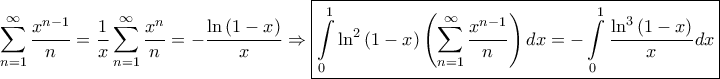
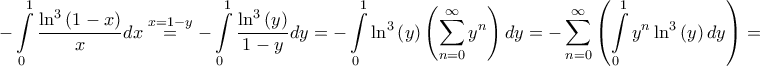
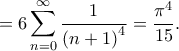
Τελικά λοιπόν
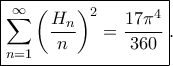
Υ.Γ Θα παραθέσω την αναλυτική λύση μου για το όριο, απλά την αφήνω λίγο στα χέρια των λυτών.
Re: Όμορφο όριο που χρειάζεται χρόνο
Παραθέτω τη λύση μου .
Θέτω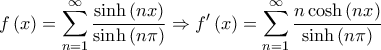
και αφού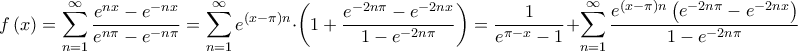
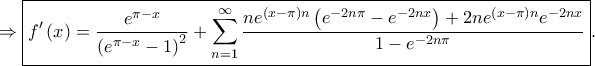
Είναι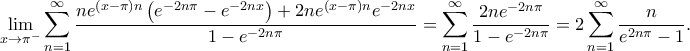
Θεωρούμε την συνάρτηση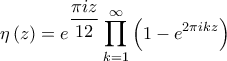 με
με  και
και 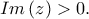 Ως γνωστό
Ως γνωστό 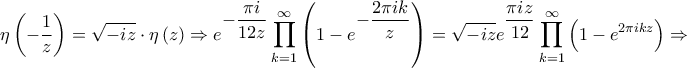
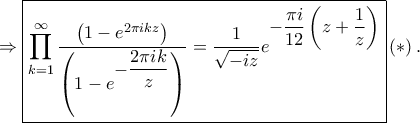
 Θέτοντας
Θέτοντας 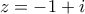 στην
στην 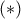 παίρνουμε
παίρνουμε ![\displaystyle \prod_{k=1}^{\infty}\frac{\left ( 1-e^{-2\pi k} \right )}{\left ( 1-\left ( -1 \right )^{k}e^{-\pi k} \right )}=\frac{\left ( 1-e^{-2\pi } \right )\left ( 1-e^{-4\pi } \right )\left ( 1-e^{-6\pi } \right )\left ( 1-e^{-8\pi } \right )...}{\left ( 1+e^{-\pi } \right )\left ( 1-e^{-2\pi } \right )\left ( 1+e^{-3\pi } \right )\left ( 1-e^{-4\pi } \right )...}=\frac{e^{\pi /24}}{\sqrt[4]{2}} \displaystyle \prod_{k=1}^{\infty}\frac{\left ( 1-e^{-2\pi k} \right )}{\left ( 1-\left ( -1 \right )^{k}e^{-\pi k} \right )}=\frac{\left ( 1-e^{-2\pi } \right )\left ( 1-e^{-4\pi } \right )\left ( 1-e^{-6\pi } \right )\left ( 1-e^{-8\pi } \right )...}{\left ( 1+e^{-\pi } \right )\left ( 1-e^{-2\pi } \right )\left ( 1+e^{-3\pi } \right )\left ( 1-e^{-4\pi } \right )...}=\frac{e^{\pi /24}}{\sqrt[4]{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/410b0d5a6b21217843aabe3dbeeb3a84.png)
![\displaystyle \Rightarrow \boxed{\prod_{k=1}^{\infty}\left ( 1+e^{\left ( 1-2k \right )\pi } \right )=\sqrt[4]{2}e^{-\pi /24}}\left ( 1 \right ). \displaystyle \Rightarrow \boxed{\prod_{k=1}^{\infty}\left ( 1+e^{\left ( 1-2k \right )\pi } \right )=\sqrt[4]{2}e^{-\pi /24}}\left ( 1 \right ).](/forum/ext/geomar/texintegr/latexrender/pictures/a6347d5bad5c8125e4147400ca3a03b8.png)
 Θέτοντας
Θέτοντας 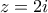 στην
στην 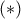 παίρνουμε
παίρνουμε 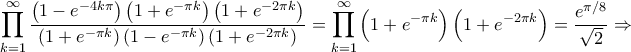
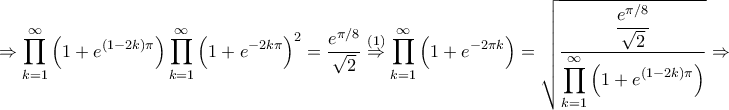
![\displaystyle \Rightarrow \prod_{k=1}^{\infty}\left ( 1+e^{-2\pi k} \right )=2^{\displaystyle -\frac{3}{8}}e^{\displaystyle \frac{\pi }{12}}\overset{\left ( 1 \right )}\Rightarrow \boxed{\prod_{k=1}^{\infty}\left ( 1+e^{-\pi k} \right )=\prod_{k=1}^{\infty}\left ( 1+e^{\left ( 1-2k \right )\pi } \right )\prod_{k=1}^{\infty}\left ( 1+e^{-2\pi k} \right )=\frac{e^{\displaystyle \frac{\pi }{24}}}{\sqrt[8]{2}}}. \displaystyle \Rightarrow \prod_{k=1}^{\infty}\left ( 1+e^{-2\pi k} \right )=2^{\displaystyle -\frac{3}{8}}e^{\displaystyle \frac{\pi }{12}}\overset{\left ( 1 \right )}\Rightarrow \boxed{\prod_{k=1}^{\infty}\left ( 1+e^{-\pi k} \right )=\prod_{k=1}^{\infty}\left ( 1+e^{\left ( 1-2k \right )\pi } \right )\prod_{k=1}^{\infty}\left ( 1+e^{-2\pi k} \right )=\frac{e^{\displaystyle \frac{\pi }{24}}}{\sqrt[8]{2}}}.](/forum/ext/geomar/texintegr/latexrender/pictures/ed034c17e1922989897fd9d41b496bb0.png)
Συνεπώς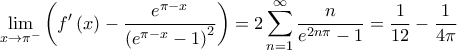
και άρα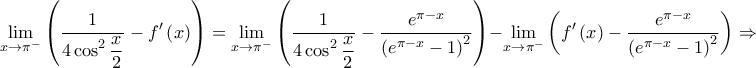
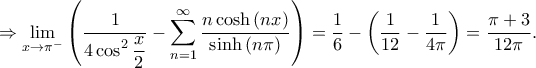
Αφού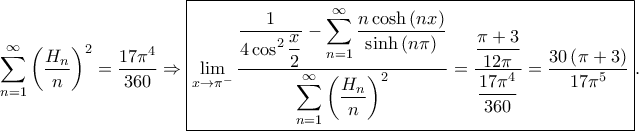
Θέτω
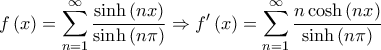
και αφού
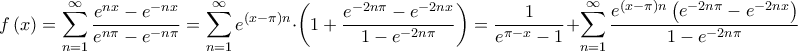
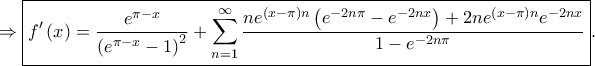
Είναι
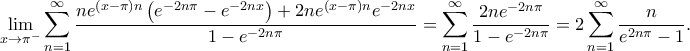
Θεωρούμε την συνάρτηση
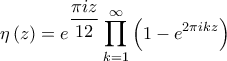 με
με  και
και 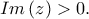 Ως γνωστό
Ως γνωστό 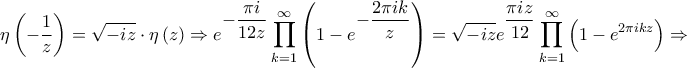
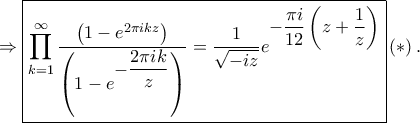
 Θέτοντας
Θέτοντας 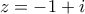 στην
στην 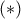 παίρνουμε
παίρνουμε ![\displaystyle \prod_{k=1}^{\infty}\frac{\left ( 1-e^{-2\pi k} \right )}{\left ( 1-\left ( -1 \right )^{k}e^{-\pi k} \right )}=\frac{\left ( 1-e^{-2\pi } \right )\left ( 1-e^{-4\pi } \right )\left ( 1-e^{-6\pi } \right )\left ( 1-e^{-8\pi } \right )...}{\left ( 1+e^{-\pi } \right )\left ( 1-e^{-2\pi } \right )\left ( 1+e^{-3\pi } \right )\left ( 1-e^{-4\pi } \right )...}=\frac{e^{\pi /24}}{\sqrt[4]{2}} \displaystyle \prod_{k=1}^{\infty}\frac{\left ( 1-e^{-2\pi k} \right )}{\left ( 1-\left ( -1 \right )^{k}e^{-\pi k} \right )}=\frac{\left ( 1-e^{-2\pi } \right )\left ( 1-e^{-4\pi } \right )\left ( 1-e^{-6\pi } \right )\left ( 1-e^{-8\pi } \right )...}{\left ( 1+e^{-\pi } \right )\left ( 1-e^{-2\pi } \right )\left ( 1+e^{-3\pi } \right )\left ( 1-e^{-4\pi } \right )...}=\frac{e^{\pi /24}}{\sqrt[4]{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/410b0d5a6b21217843aabe3dbeeb3a84.png)
![\displaystyle \Rightarrow \boxed{\prod_{k=1}^{\infty}\left ( 1+e^{\left ( 1-2k \right )\pi } \right )=\sqrt[4]{2}e^{-\pi /24}}\left ( 1 \right ). \displaystyle \Rightarrow \boxed{\prod_{k=1}^{\infty}\left ( 1+e^{\left ( 1-2k \right )\pi } \right )=\sqrt[4]{2}e^{-\pi /24}}\left ( 1 \right ).](/forum/ext/geomar/texintegr/latexrender/pictures/a6347d5bad5c8125e4147400ca3a03b8.png)
 Θέτοντας
Θέτοντας 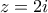 στην
στην 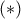 παίρνουμε
παίρνουμε 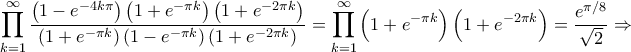
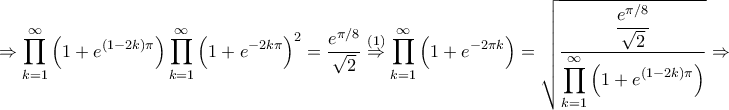
![\displaystyle \Rightarrow \prod_{k=1}^{\infty}\left ( 1+e^{-2\pi k} \right )=2^{\displaystyle -\frac{3}{8}}e^{\displaystyle \frac{\pi }{12}}\overset{\left ( 1 \right )}\Rightarrow \boxed{\prod_{k=1}^{\infty}\left ( 1+e^{-\pi k} \right )=\prod_{k=1}^{\infty}\left ( 1+e^{\left ( 1-2k \right )\pi } \right )\prod_{k=1}^{\infty}\left ( 1+e^{-2\pi k} \right )=\frac{e^{\displaystyle \frac{\pi }{24}}}{\sqrt[8]{2}}}. \displaystyle \Rightarrow \prod_{k=1}^{\infty}\left ( 1+e^{-2\pi k} \right )=2^{\displaystyle -\frac{3}{8}}e^{\displaystyle \frac{\pi }{12}}\overset{\left ( 1 \right )}\Rightarrow \boxed{\prod_{k=1}^{\infty}\left ( 1+e^{-\pi k} \right )=\prod_{k=1}^{\infty}\left ( 1+e^{\left ( 1-2k \right )\pi } \right )\prod_{k=1}^{\infty}\left ( 1+e^{-2\pi k} \right )=\frac{e^{\displaystyle \frac{\pi }{24}}}{\sqrt[8]{2}}}.](/forum/ext/geomar/texintegr/latexrender/pictures/ed034c17e1922989897fd9d41b496bb0.png)
Συνεπώς
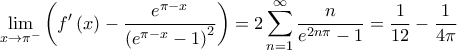
και άρα
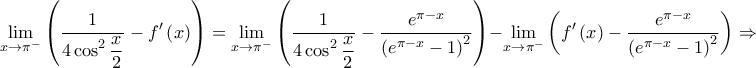
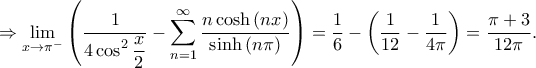
Αφού
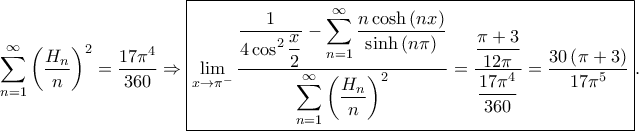
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Όμορφο όριο που χρειάζεται χρόνο
Δημήτρη,
το παραπάνω βήμα θέλει αιτιολόγιση: Περνάς το όριο μέσα στο άθροισμα. Όμως, πρόκειται για απειροάθροισμα, που σημαίνει ότι η εναλλαγή ορίου και άθροισης δεν ισχύει πάντα. Δεν ξέρω τι γίνεται στην συγκεκριμένη περίπτωση (δεν το κοίταξα) αλλά σίγουρα θέλει έλεγχο.
Re: Όμορφο όριο που χρειάζεται χρόνο
Γεια σας .Mihalis_Lambrou έγραψε: ↑Παρ Ιαν 05, 2024 7:02 pmΔημήτρη,
το παραπάνω βήμα θέλει αιτιολόγιση: Περνάς το όριο μέσα στο άθροισμα. Όμως, πρόκειται για απειροάθροισμα, που σημαίνει ότι η εναλλαγή ορίου και άθροισης δεν ισχύει πάντα. Δεν ξέρω τι γίνεται στην συγκεκριμένη περίπτωση (δεν το κοίταξα) αλλά σίγουρα θέλει έλεγχο.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης