
ώστε να ισχύουν
1)

2)

κατόπιν βρείτε αν υπάρχουν τα όρια

μέχρι 10-4-2019
Συντονιστής: Demetres





 συνεχής συνάρτηση με την ιδιότητα
συνεχής συνάρτηση με την ιδιότητα 

 στο
στο  .
.
 να μηδενίζεται.
να μηδενίζεται.
 υπάρχει στο
υπάρχει στο 


 υπάρχει.
υπάρχει. θα βγεί
θα βγεί  που είναι ΑΤΟΠΟ.
που είναι ΑΤΟΠΟ.
 συνεχῶς διαφορίσιμη, τότε τὸ ΠΑΤ
συνεχῶς διαφορίσιμη, τότε τὸ ΠΑΤ
 , ὥστε
, ὥστε 
 , δηλαδὴ ὁρισμένη σ᾽ ὅλο τὸ
, δηλαδὴ ὁρισμένη σ᾽ ὅλο τὸ  .
. καὶ ὑπάρχουν
καὶ ὑπάρχουν  , ὥστε
, ὥστε  , καὶ
, καὶ  , τότε
, τότε

 καὶ ὑπάρχει μοναδικὀ
καὶ ὑπάρχει μοναδικὀ 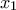 , ὥστε
, ὥστε  , καὶ
, καὶ  , τότε
, τότε

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες