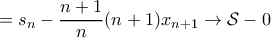Σελίδα 1 από 1
Σύγκλιση σειράς
Δημοσιεύτηκε: Κυρ Απρ 05, 2020 3:10 pm
από Tolaso J Kos
Re: Σύγκλιση σειράς
Δημοσιεύτηκε: Κυρ Απρ 05, 2020 7:04 pm
από Mihalis_Lambrou
1) Έστω

η ακολουθία των μερικών αθροισμάτων της σειράς, οπότε

. Από Cesaro

, δηλαδή

.
Επίσης από υπόθεση

. Αφαιρώντας τις δύο έπεται

. Όμως από την

και Cesaro, το τελευταίο άθροισμα τείνει στο

. Από μοναδικότητα του ορίου,

.
2) Παίρνουμε

αν

όπου

, και
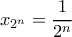
αλλιώς. Τώρα η σειρά συγκλίνει αλλά αφού

και

, η ακολουθία

δεν συγκλίνει.
3)

4) Πρέπει να κλείσω. Θα επανέλθω αργότερα. Συγγνώμη. Για την ώρα σημειώνω μονάχα ότι έχει τυπογραφικό σφάλμα: Tο

πρέπει να γίνει

.
Re: Σύγκλιση σειράς
Δημοσιεύτηκε: Κυρ Απρ 05, 2020 7:40 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
Τόλη ξέχασες να βάλεις ημερομηνία και δεν το πήρε χαμπάρι ο Μιχάλης.
Δεν θα γράψω την λύση του τελευταίου μήπως την γράψει κανένας φοιτητής.
Θα κάνω μία απλούστερη λύση για το πρώτο.
Αν

και το άπειρο μέσα τότε υπάρχει

ώστε για

να έχουμε

.
(αν είναι άπειρο το
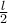
το κάνω ένα θετικό αριθμό)
Αφού η αρμονική αποκλίνει θα αποκλίνει ΑΤΟΠΟ.
Αν

θεωρούμε την

και πέφτουμε στην πρώτη περίπτωση
Re: Σύγκλιση σειράς
Δημοσιεύτηκε: Κυρ Απρ 05, 2020 7:44 pm
από Mihalis_Lambrou
Tolaso J Kos έγραψε: ↑Κυρ Απρ 05, 2020 3:10 pm
[*]Να δειχθεί ότι αν η

συγκλίνει και η

είναι φθίνουσα τότε:

Συνεχίζω από εκεί που έμεινα. Το κάνω για το
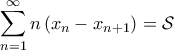
, δηλαδή με διόρθωση του τυπογραφικού σφάλματος της εκφώνησης.
Aν

φθίνουσα (αναγκαστικά στο

) είναι απλό και γνωστό ότι

. Θα το βρει κανείς σε όλα τα βιβλία με σειρές (το πρώτο και κύριο βήμα είναι

.
Αν

το μερικό άθροισμα της αριστερής σειράς, έχουμε

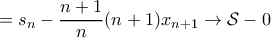 Ωχχχχ. Tώρα βλέπω το μήνυμα του Σταύρου (δεν υπήρχε όταν ξεκίνησα να γράφω) και τώρα αντιλήφθηκα ότι ήταν άσκηση για φοιτητές. Ωχχχχ.
Ωχχχχ. Tώρα βλέπω το μήνυμα του Σταύρου (δεν υπήρχε όταν ξεκίνησα να γράφω) και τώρα αντιλήφθηκα ότι ήταν άσκηση για φοιτητές. Ωχχχχ.
Re: Σύγκλιση σειράς
Δημοσιεύτηκε: Κυρ Απρ 05, 2020 8:34 pm
από Tolaso J Kos
Mihalis_Lambrou έγραψε: ↑Κυρ Απρ 05, 2020 7:44 pm
... και τώρα αντιλήφθηκα ότι ήταν άσκηση για φοιτητές. Ωχχχχ.
Δε πειράζει.. Δεν έγινε και κάτι.
 όπου
όπου  πραγματική ακολουθία και έστω
πραγματική ακολουθία και έστω  .
. όπου
όπου  πραγματική ακολουθία και έστω
πραγματική ακολουθία και έστω  .
. συγκλίνει και το
συγκλίνει και το  υπάρχει ( πεπερασμένο ή άπειρο ) τότε
υπάρχει ( πεπερασμένο ή άπειρο ) τότε  .
. , η
, η  συγκλίνει αλλά το
συγκλίνει αλλά το  δεν υπάρχει.
δεν υπάρχει. ,
,  αλλά η
αλλά η  αποκλίνει.
αποκλίνει. συγκλίνει και η
συγκλίνει και η  είναι φθίνουσα τότε:
είναι φθίνουσα τότε:
 η ακολουθία των μερικών αθροισμάτων της σειράς, οπότε
η ακολουθία των μερικών αθροισμάτων της σειράς, οπότε  . Από Cesaro
. Από Cesaro  , δηλαδή
, δηλαδή  .
. . Αφαιρώντας τις δύο έπεται
. Αφαιρώντας τις δύο έπεται  . Όμως από την
. Όμως από την  και Cesaro, το τελευταίο άθροισμα τείνει στο
και Cesaro, το τελευταίο άθροισμα τείνει στο  . Από μοναδικότητα του ορίου,
. Από μοναδικότητα του ορίου,  .
. αν
αν  όπου
όπου  , και
, και 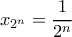 αλλιώς. Τώρα η σειρά συγκλίνει αλλά αφού
αλλιώς. Τώρα η σειρά συγκλίνει αλλά αφού  και
και  , η ακολουθία
, η ακολουθία  δεν συγκλίνει.
δεν συγκλίνει.
 πρέπει να γίνει
πρέπει να γίνει  .
.
 ώστε για
ώστε για 
 .
.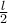 το κάνω ένα θετικό αριθμό)
το κάνω ένα θετικό αριθμό) θεωρούμε την
θεωρούμε την 
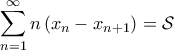 , δηλαδή με διόρθωση του τυπογραφικού σφάλματος της εκφώνησης.
, δηλαδή με διόρθωση του τυπογραφικού σφάλματος της εκφώνησης.  φθίνουσα (αναγκαστικά στο
φθίνουσα (αναγκαστικά στο  ) είναι απλό και γνωστό ότι
) είναι απλό και γνωστό ότι  . Θα το βρει κανείς σε όλα τα βιβλία με σειρές (το πρώτο και κύριο βήμα είναι
. Θα το βρει κανείς σε όλα τα βιβλία με σειρές (το πρώτο και κύριο βήμα είναι  .
.  το μερικό άθροισμα της αριστερής σειράς, έχουμε
το μερικό άθροισμα της αριστερής σειράς, έχουμε