Πολύ ωραία.giannispapav έγραψε: ↑Τρί Μαρ 12, 2024 11:26 pm
Μπορούμε, μετά από μετατόπιση και στροφή (που είναι ομοιομορφισμοί), να υποθέσουμε ότι η εξίσωση της έλλειψης παίρνει τη μορφήοπότε αν
είναι ο μοναδιαίος κύκλος, τότε η
με
είναι ομοιμορφισμός.
Ασκήσεις Τοπολογίας
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
Re: Ασκήσεις Τοπολογίας
Κωνσταντίνος Σμπώκος
Λέξεις Κλειδιά:
Re: Ασκήσεις Τοπολογίας
15)
Έστω δύο μετρικοί χώροι . Έστω η μετρική
. Έστω η μετρική  στον
στον  με
με  .
.
Δείξτε ότι ο μετρικός χώρος είναι τοπολογικά ο χώρος γινόμενο των
είναι τοπολογικά ο χώρος γινόμενο των  και
και 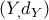 . Δηλαδή ότι έχουν την ίδια τοπολογία.
. Δηλαδή ότι έχουν την ίδια τοπολογία.
Έστω δύο μετρικοί χώροι
 . Έστω η μετρική
. Έστω η μετρική  στον
στον  με
με  .
.Δείξτε ότι ο μετρικός χώρος
 είναι τοπολογικά ο χώρος γινόμενο των
είναι τοπολογικά ο χώρος γινόμενο των  και
και 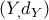 . Δηλαδή ότι έχουν την ίδια τοπολογία.
. Δηλαδή ότι έχουν την ίδια τοπολογία.Κωνσταντίνος Σμπώκος
-
Ιάσων Κωνσταντόπουλος
- Δημοσιεύσεις: 38
- Εγγραφή: Κυρ Ιαν 28, 2024 10:16 pm
- Επικοινωνία:
Re: Ασκήσεις Τοπολογίας
Έστω
 οι τοπολογίες των
οι τοπολογίες των  αντίστοιχα,
αντίστοιχα,  η τοπολογία του
η τοπολογία του 
και
 η τοπολογία του γινομένου των
η τοπολογία του γινομένου των 
Μια βάση για την
 αποτελεί το σύνολο
αποτελεί το σύνολο 
Μια βάση για την
 αποτελεί το σύνολο
αποτελεί το σύνολο 
Μια βάση για την
 αποτελεί το σύνολο
αποτελεί το σύνολο 
Μια υποβάση (εξ' ορισμού) για την
 αποτελεί η ένωση
αποτελεί η ένωση 
Θεωρώντας τις πεπερασμένες τομές των μελών της λαμβάνουμε για την
 την ακόλουθη βάση
την ακόλουθη βάση 
και από αυτήν βρίσκουμε ότι:
Μια βάση για την
 αποτελεί το σύνολο
αποτελεί το σύνολο 
Έστω

1. Από τον εγκλεισμό

 έχουμε
έχουμε 
2. Από τον εγκλεισμό
 έχουμε
έχουμε 
Οπότε λαμβάνουμε

Ιάσων Κωνσταντόπουλος
Re: Ασκήσεις Τοπολογίας
16) Είναι γενικά γνωστό ότι αν  οικογένεια τοπολογιών στο σύνολο
οικογένεια τοπολογιών στο σύνολο  , τότε
, τότε  τοπολογία στο
τοπολογία στο  . Είναι άραγε πάντα αλήθεια ότι, αν
. Είναι άραγε πάντα αλήθεια ότι, αν  οικογένεια μετρικών τοπολογιών στο
οικογένεια μετρικών τοπολογιών στο  , τότε
, τότε  μετρική τοπολογία στο
μετρική τοπολογία στο  ;
;
 οικογένεια τοπολογιών στο σύνολο
οικογένεια τοπολογιών στο σύνολο  , τότε
, τότε  τοπολογία στο
τοπολογία στο  . Είναι άραγε πάντα αλήθεια ότι, αν
. Είναι άραγε πάντα αλήθεια ότι, αν  οικογένεια μετρικών τοπολογιών στο
οικογένεια μετρικών τοπολογιών στο  , τότε
, τότε  μετρική τοπολογία στο
μετρική τοπολογία στο  ;
;-
Ιάσων Κωνσταντόπουλος
- Δημοσιεύσεις: 38
- Εγγραφή: Κυρ Ιαν 28, 2024 10:16 pm
- Επικοινωνία:
Re: Ασκήσεις Τοπολογίας
Η απάντηση φαίνεται πως είναι αρνητική.
Έστω
 ,
,  η ευκλείδεια μετρική και
η ευκλείδεια μετρική και  η τοπολογία της
η τοπολογία της 
Θεωρούμε την 1-1 και επί συνάρτηση
 με
με 
Έστω
 η μετρική στο
η μετρική στο  που καθιστά την
που καθιστά την  ισομετρία, ήτοι
ισομετρία, ήτοι  και
και  η τοπολογία της.
η τοπολογία της.Η
 θα είναι και ομοιομορφισμός μεταξύ των τοπολογικών χώρων
θα είναι και ομοιομορφισμός μεταξύ των τοπολογικών χώρων  ,
, 
οπότε

Θεωρούμε την τομή των δυο τοπολογιών

Η
 δεν είναι μετρήσιμη τοπολογία στο
δεν είναι μετρήσιμη τοπολογία στο  επειδή ο
επειδή ο  δεν είναι Hausdorff.
δεν είναι Hausdorff.Συγκεκριμένα θα δείξουμε ότι:
για
 αν
αν  οποιαδήποτε ανοιχτά σύνολα του
οποιαδήποτε ανοιχτά σύνολα του  με
με  και
και  τότε
τότε  .
.Επειδή
 θα υπάρχει
θα υπάρχει  ώστε
ώστε  και
και  .
.Επειδή
 θα πρέπει
θα πρέπει  για κάποιο
για κάποιο 
Επειδή
 θα έχουμε
θα έχουμε  οπότε
οπότε 
Επειδή
 θα υπάρχει
θα υπάρχει  ώστε
ώστε 
Όμως
 και
και  οπότε
οπότε  , επομένως
, επομένως 
Κατά συνέπεια ο
 δεν είναι Hausdorff οπότε δεν είναι μετρήσιμος
δεν είναι Hausdorff οπότε δεν είναι μετρήσιμος 
Σημείωση
Ο χώρος
 έχει μη τετριμμένα ανοιχτά σύνολα. Για παράδειγμα αν
έχει μη τετριμμένα ανοιχτά σύνολα. Για παράδειγμα αν  και
και  το σύνολο
το σύνολο 
είναι ανοιχτό. Πράγματι,
 και
και  οπότε
οπότε 
Ιάσων Κωνσταντόπουλος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
