abfx έγραψε: ↑Κυρ Φεβ 18, 2024 1:56 pm
12) Έστω

σύνολο και

. Θέτουμε:
 (Τοπολογία εξαιρουμένου σημείου)
(Τοπολογία εξαιρουμένου σημείου)
 (Συμπεπερασμένη τοπολογία)
(Συμπεπερασμένη τοπολογία)
α) Να δειχθεί ότι η

τοπολογία του

.
b) Αν επιπλέον

(άπειρο) αριθμήσιμο, να δειχθεί ότι

μετρικοποιήσιμος.
α)
Καταρχήν προφανώς

.
Επιπλέον αν έχουμε μια οικογένεια

συνόλων στην

(μπορούμε να υποθέσουμε ότι κανένα από τα

δεν ταυτίζεται με το

η το

) και η ένωση τους δεν ανήκει στην

τότε υπάρχει

ώστε

και επιπλέον όλα τα

έχουν άπειρο συμπλήρωμα. Άρα το σύνολο

δεν ανήκει στην

. Άτοπο.
Αν πάρουμε δύο σύνολα

που το συπλήρωμά τους ανήκει στην

τότε αν το συμπλήρωμα της τομής τους δεν ανήκει στην

, τότε θα έχουμε ότι

και

Άρα τα

είναι και τα δυο άπειρα σύνολα και κάποιο από τα δυο δεν περιέχει το

(έστω το

).
Άρα το συμπλήρωμα του

περιέχει το

. Άρα αφού το συμπλήρωμα του

είναι ανοιχτό θα πρέπει να έχει πεπερασμένο συμπλήρωμα.
Άρα το

είναι πεπερασμένο. Άτοπο.
Συνεπώς δείξαμε ότι τη ένωση είναι τοπολογία.
β)
Παίρνουμε την μετρική

αν

και

, αν

. Τέλος ορίζουμε

.
Μπορούμε να δείξουμε διακρίνοντας περιπτώσεις(δεν θα το κάνω) ότι πρόκειται για μια μετρική.
Θα δείξω ότι αυτή η μετρική επάγει την

.
Αρχικά, θα δείξω ότι όλες οι ανοιχτές μπάλες ανήκουν στην

.
Παίρνω μια μπάλα

. Αρχικά αν

εύκολα βλέπουμε ότι το συμπλήρωμα της μπάλας είναι πεπερασμένο.
Αν

, τότε αν το

ανήκει στην μπάλα έχουμε

.
Άρα πόσα

δεν ανήκουν στην μπάλα; Δηλαδή για πόσα

ισχύει

.
Προφανώς πεπερασμένα το πλήθος.
Άρα έχουμε δείξει ότι όλες οι μπάλες ανήκουν στην

.
Τώρα για να τελειώσουμε, θα δείξουμε ότι κάθε σύνολο της

γράφεται ως ένωση ανοιχτών μπαλών.
Παίρνω

.
Αν

έχουμε

. Tελειώσαμε.
Αν

, έχουμε ότι το συμπλήρωμα του

είναι πεπερασμένο. Έστω λοιπόν ότι τα στοιχεία που δεν ανήκουν στο

είναι τα

με

.
Tότε έχουμε

.
Τέλος.
οι
και
είναι ομοτοπικά ισοδύναμοι.
είναι ομοιομορφισμός, τότε έχουμε ομοιομορφισμό
.
και
είναι ομοτοπικά ισοδύναμοι. Άρα έχουμε ομοτοπική ισοδυναμία
και άρα
.
 και
και  δεν μπορεί να είναι ομοτοπικά ισοδύναμοι για
δεν μπορεί να είναι ομοτοπικά ισοδύναμοι για  γιατί αλλιώς θα είχαν ισόμορφες ομάδες ομολογίας κάθε τάξης, κάτι που δεν μπορεί να ισχύει.
γιατί αλλιώς θα είχαν ισόμορφες ομάδες ομολογίας κάθε τάξης, κάτι που δεν μπορεί να ισχύει.
 μια συνεκτική τοπολογική πολλαπλότητα διαστάσεως
μια συνεκτική τοπολογική πολλαπλότητα διαστάσεως  . Έστω
. Έστω  ένας (μεγιστικός) τοπολογικός άτλας της πολλαπλότητας. Σταθεροποιούμε
ένας (μεγιστικός) τοπολογικός άτλας της πολλαπλότητας. Σταθεροποιούμε  και ονομάζουμε
και ονομάζουμε ![\Omega = \{p \in X | \exists \gamma \in \mathcal{C}([0,1],X), \gamma(0) = p_{0} \hspace{2mm} \gamma(1) = p\} \Omega = \{p \in X | \exists \gamma \in \mathcal{C}([0,1],X), \gamma(0) = p_{0} \hspace{2mm} \gamma(1) = p\}](/forum/ext/geomar/texintegr/latexrender/pictures/703a33e5ade26da7b3b9b6b7830484f1.png) . Θα αποδείξουμε ότι το σύνολο
. Θα αποδείξουμε ότι το σύνολο  είναι ένα μη κενό, ανοικτό και κλειστό υποσύνολο του
είναι ένα μη κενό, ανοικτό και κλειστό υποσύνολο του  από όπου άμεσα έπεται ότι η
από όπου άμεσα έπεται ότι η  τέτοιο ώστε
τέτοιο ώστε  . Προφανώς, το
. Προφανώς, το  είναι ένα ανοικτό υποσύνολο του χώρου
είναι ένα ανοικτό υποσύνολο του χώρου  και άρα μπορούμε να βρούμε ανοικτή μπάλα
και άρα μπορούμε να βρούμε ανοικτή μπάλα  με αρκούντως μικρή ακτίνα και κέντρο το
με αρκούντως μικρή ακτίνα και κέντρο το 
 . Συνεπώς το
. Συνεπώς το  είναι μια κατά τόξα συνεκτική ανοικτή περιοχή του περιοχή του
είναι μια κατά τόξα συνεκτική ανοικτή περιοχή του περιοχή του  . Επομένως
. Επομένως  , που σημαίνει ότι
, που σημαίνει ότι  .
. τότε υπάρχει μια συνεχής απεικόνιση
τότε υπάρχει μια συνεχής απεικόνιση ![\gamma_{1} \in \mathcal{C}([0,1],X) \gamma_{1} \in \mathcal{C}([0,1],X)](/forum/ext/geomar/texintegr/latexrender/pictures/52a1ec6743086448aac3bf96ab2b43e9.png) με
με  και
και  .Όπως σχολιάσαμε και προηγουμένως υπάρχει μια ανοικτή και κατά τόξα συνεκτική περιοχή,
.Όπως σχολιάσαμε και προηγουμένως υπάρχει μια ανοικτή και κατά τόξα συνεκτική περιοχή,  , του
, του  . Αν
. Αν  τυχόν, τότε υπάρχει
τυχόν, τότε υπάρχει ![\gamma_{2} \in \mathcal{C}([0,1],X) \gamma_{2} \in \mathcal{C}([0,1],X)](/forum/ext/geomar/texintegr/latexrender/pictures/d5dae033f3fd750951954f5c659a610c.png) με αρχή το
με αρχή το  . Θεωρούμε τη καμπύλη
. Θεωρούμε τη καμπύλη  , η οποία και προκύπτει από το σύνηθες γινόμενο διαδοχικών καμπυλών. Προφανώς, η
, η οποία και προκύπτει από το σύνηθες γινόμενο διαδοχικών καμπυλών. Προφανώς, η  είναι συνεχής και έχει αρχή το
είναι συνεχής και έχει αρχή το  και αφού το
και αφού το  . Πράγματι λοιπόν το
. Πράγματι λοιπόν το  είναι ανοικτό. Ας είναι
είναι ανοικτό. Ας είναι  τυχόν και ας υποθέσουμε προς άτοπο ότι για μια κατά τόξα συνεκτική και ανοικτή περιοχή του
τυχόν και ας υποθέσουμε προς άτοπο ότι για μια κατά τόξα συνεκτική και ανοικτή περιοχή του  του
του  ισχύει
ισχύει  . Τότε, όπως δείξαμε προηγουμένως μπορούμε να βρούμε ένα μονοπάτι από το
. Τότε, όπως δείξαμε προηγουμένως μπορούμε να βρούμε ένα μονοπάτι από το  , κάτι που φυσικά δεν μπορεί να ισχύει. Επομένως το
, κάτι που φυσικά δεν μπορεί να ισχύει. Επομένως το  ,
,  και
και  .
.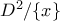 είναι απλά συνεκτικός αν και μόνο αν
είναι απλά συνεκτικός αν και μόνο αν  .
. και ορίζουμε τον χώρο
και ορίζουμε τον χώρο  .
. είναι εσωτερικό σημείο του
είναι εσωτερικό σημείο του  . Είναι εύκολο να δούμε ότι ο χώρος
. Είναι εύκολο να δούμε ότι ο χώρος  και άρα οι θεμελιώδεις ομάδες τους είναι ισόμορφες. Αφού η θεμελιώδεις ομάδα του κύκλου είναι άπειρη κυκλική ομάδα, έπεται ότι ο χώρος
και άρα οι θεμελιώδεις ομάδες τους είναι ισόμορφες. Αφού η θεμελιώδεις ομάδα του κύκλου είναι άπειρη κυκλική ομάδα, έπεται ότι ο χώρος  . Είναι εύκολο να δούμε τότε ότι ο χώρος
. Είναι εύκολο να δούμε τότε ότι ο χώρος  . Απο εδώ και στο εξής δουλεύουμε στο μιγαδικό επίπεδο.
. Απο εδώ και στο εξής δουλεύουμε στο μιγαδικό επίπεδο. που ορίζεται ως εξής
που ορίζεται ως εξής  . Προφανώς η
. Προφανώς η  είναι συνεχής, 1-1 και επί του συνόλου των μιγαδικών αριθμών με θετικό πραγματικό μέρος. Έτσι παίρνουμε έναν ομοιομορφισμό μεταξύ του
είναι συνεχής, 1-1 και επί του συνόλου των μιγαδικών αριθμών με θετικό πραγματικό μέρος. Έτσι παίρνουμε έναν ομοιομορφισμό μεταξύ του  και ενός κλειστού ημιεπιπέδου
και ενός κλειστού ημιεπιπέδου στο
στο  , όπου
, όπου  μετρικοποιήσιμος(metrizable) τοπολογικός χώρος;
μετρικοποιήσιμος(metrizable) τοπολογικός χώρος; με
με  , τότε είναι μετρικοποιήσιμος.
, τότε είναι μετρικοποιήσιμος. .
. σύνολο και
σύνολο και  . Θέτουμε:
. Θέτουμε:
 (Τοπολογία εξαιρουμένου σημείου)
(Τοπολογία εξαιρουμένου σημείου) (Συμπεπερασμένη τοπολογία)
(Συμπεπερασμένη τοπολογία) τοπολογία του
τοπολογία του  (άπειρο) αριθμήσιμο, να δειχθεί ότι
(άπειρο) αριθμήσιμο, να δειχθεί ότι  μετρικοποιήσιμος.
μετρικοποιήσιμος. .
. συνόλων στην
συνόλων στην  δεν ταυτίζεται με το
δεν ταυτίζεται με το  η το
η το  ώστε
ώστε  και επιπλέον όλα τα
και επιπλέον όλα τα  δεν ανήκει στην
δεν ανήκει στην  που το συπλήρωμά τους ανήκει στην
που το συπλήρωμά τους ανήκει στην  και
και 
 (έστω το
(έστω το  ).
). αν
αν  και
και  , αν
, αν  . Τέλος ορίζουμε
. Τέλος ορίζουμε  .
. . Αρχικά αν
. Αρχικά αν  εύκολα βλέπουμε ότι το συμπλήρωμα της μπάλας είναι πεπερασμένο.
εύκολα βλέπουμε ότι το συμπλήρωμα της μπάλας είναι πεπερασμένο. .
. δεν ανήκουν στην μπάλα; Δηλαδή για πόσα
δεν ανήκουν στην μπάλα; Δηλαδή για πόσα  .
. .
. έχουμε
έχουμε  . Tελειώσαμε.
. Tελειώσαμε. , έχουμε ότι το συμπλήρωμα του
, έχουμε ότι το συμπλήρωμα του  με
με  .
. .
. .
. .
. τότε
τότε  , για να είναι ολοκληρωμένη η απόδειξη.
, για να είναι ολοκληρωμένη η απόδειξη. . Τότε
. Τότε  και
και  .
. .
.
 , έχουμε
, έχουμε  .
. , όμως
, όμως  .
. και
και  τότε
τότε  οπότε τα
οπότε τα  τότε υπάρχει
τότε υπάρχει  (επιλογή) ώστε
(επιλογή) ώστε  .
. . Πάει και αυτό.
. Πάει και αυτό. .
. . Επειδή αυτή η τομή είναι πεπερασμένη παίρνουμε ότι το
. Επειδή αυτή η τομή είναι πεπερασμένη παίρνουμε ότι το  στην περίπτωση που το συμπλήρωμα του συνόλου
στην περίπτωση που το συμπλήρωμα του συνόλου  ώστε η μπάλα
ώστε η μπάλα  να μην περιέχει κανένα από τα στοιχεία που δεν ανήκουν στο σύνολο
να μην περιέχει κανένα από τα στοιχεία που δεν ανήκουν στο σύνολο  υπάρχει το ελάχιστο ανοιχτό σύνολο που περιέχει το
υπάρχει το ελάχιστο ανοιχτό σύνολο που περιέχει το  του μοναδιαίου κύκλου και ότι βρίσκεται έξω από τον κύκλο. Φέρνοντας τυχούσα ημιευθεία από το κέντρο του κύκλου, αυτή τέμνει τον κύκλο και την έλλειψη στα σημεία
του μοναδιαίου κύκλου και ότι βρίσκεται έξω από τον κύκλο. Φέρνοντας τυχούσα ημιευθεία από το κέντρο του κύκλου, αυτή τέμνει τον κύκλο και την έλλειψη στα σημεία  και
και  αντίστοιχα. Αυτή όμως είναι μια 1-1, συνεχής αντιστοίχιση των σημείων του κύκλου με τα σημεία της έλλειψης. Προφανώς η αντίστροφή της απεικόνιση είναι, επίσης, συνεχής.
αντίστοιχα. Αυτή όμως είναι μια 1-1, συνεχής αντιστοίχιση των σημείων του κύκλου με τα σημεία της έλλειψης. Προφανώς η αντίστροφή της απεικόνιση είναι, επίσης, συνεχής. 
 οπότε αν
οπότε αν  είναι ο μοναδιαίος κύκλος, τότε η
είναι ο μοναδιαίος κύκλος, τότε η  με
με  είναι ομοιμορφισμός.
είναι ομοιμορφισμός. , θέτουμε
, θέτουμε  .
. και επιπλέον
και επιπλέον  :
:  .
. και προφανώς
και προφανώς  ,
,  , δηλαδή
, δηλαδή  . Ορίζουμε
. Ορίζουμε ![f:[0,1]\rightarrow A f:[0,1]\rightarrow A](/forum/ext/geomar/texintegr/latexrender/pictures/efbfcf7516c63888494dcbd758ac85cf.png) ως εξής:
ως εξής:![f(t)=
\begin{cases}
a & \text{, }t\in \big{[} 0, \frac{1}{3} \big{)}\\
x & \text{, }t\in \big{[} \frac{1}{3}, \frac{2}{3}\big{]}\\
b & \text{, }t\in \big{(} \frac{2}{3},1\big{]} \\
\end{cases} f(t)=
\begin{cases}
a & \text{, }t\in \big{[} 0, \frac{1}{3} \big{)}\\
x & \text{, }t\in \big{[} \frac{1}{3}, \frac{2}{3}\big{]}\\
b & \text{, }t\in \big{(} \frac{2}{3},1\big{]} \\
\end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/66e9bbe3fb54f3aa8c43f4367daccd9a.png)
 ανοιχτό.
ανοιχτό.
 , τότε
, τότε ![G=A \implies f^{-1}(G)=[0,1] G=A \implies f^{-1}(G)=[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/dded6748c7252ba99ca2cc49c75d7faa.png) , ανοιχτό (στη σχετική τοπολογία).
, ανοιχτό (στη σχετική τοπολογία). , τότε
, τότε ![f^{-1}(G) \in \{ \emptyset , \big{[} 0, \frac{1}{3} \big{)}, \big{(} \frac{2}{3},1\big{]} , \big{[} 0, \frac{1}{3} \big{)}\cup \big{(} \frac{2}{3},1\big{]} \} f^{-1}(G) \in \{ \emptyset , \big{[} 0, \frac{1}{3} \big{)}, \big{(} \frac{2}{3},1\big{]} , \big{[} 0, \frac{1}{3} \big{)}\cup \big{(} \frac{2}{3},1\big{]} \}](/forum/ext/geomar/texintegr/latexrender/pictures/f822dd5fbd7dc2e55775aa8122e52be0.png) , οπότε
, οπότε  ανοιχτό (στη σχετική τοπολογία).
ανοιχτό (στη σχετική τοπολογία). ,
,  , συνεπώς έχουμε το ζητούμενο.
, συνεπώς έχουμε το ζητούμενο.