Γράφω λύση πάνω στην ιδέα του Ροδόλφου.papel έγραψε: ↑Πέμ Ιουν 11, 2009 12:46 pmΝα δείξετε οτι εάν για κάθε x το πολυώνυμο G(x) ικανοποιει την σχεση :
τοτε το πολυωνυμο αυτο ειναι σταθερο.
(Δυσκολη και θα ηθελα να δω πως θα την αντιμετωπιζαν οι συναδελφοι οχι τοσο την λυση
αλλα το σκεπτικο πως να κινηθουμε)
Διορθωση στην εκφωνηση αντι του καθε μετα απο υποδειξεις
Εχουμε
![\displaystyle{\displaystyle G(2{x^2} - 1) = \frac{{{{\left[ {G(x)} \right]}^2}}}{2} - 1} \displaystyle{\displaystyle G(2{x^2} - 1) = \frac{{{{\left[ {G(x)} \right]}^2}}}{2} - 1}](/forum/ext/geomar/texintegr/latexrender/pictures/834662e68e1a868a2dff95bd227cbdb0.png)
Θέτοντας
 και
και 
γίνεται
 (1)
(1)Το
 είναι ένα τριγωνομετρικό πολυώνυμο.
είναι ένα τριγωνομετρικό πολυώνυμο.Εδω συγκεκριμένα είναι

Να σημειώσω ότι η (1) ισχύει για όλα τα

Αυτό οφείλεται στο ότι κάθε τριγωνομετρικό πολυώνυμο,δηλαδή μια παράσταση
της μορφής
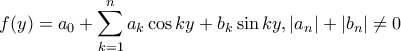
έχει στο
![[0,2\pi ] [0,2\pi ]](/forum/ext/geomar/texintegr/latexrender/pictures/58c9a5de0cb1a343ae0acd1fb191eea1.png) το πολύ
το πολύ 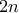 ρίζες.
ρίζες.(Θέτουμε
 και έχουμε τις ρίζες ενός μιγαδικού πολυώνυμου
και έχουμε τις ρίζες ενός μιγαδικού πολυώνυμου 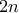 βαθμού στον
βαθμού στον μοναδιαίο κύκλο)
Από την (1) παίρνουμε ότι
α)

β)

Αν το
 τότε η α),β) δίνουν
τότε η α),β) δίνουν αν υπάρχει
 με
με  τότε
τότε 
Θα έχουμε ΑΤΟΠΟ αν εξασφαλίσουμε
 με
με 
Αλλά αυτό είναι άμεσο από το

