Mihalis_Lambrou έγραψε:
dement έγραψε: Αν τωρα επιτρεψουμε και τη δευτερη συνθηκη, τα πραγματα μπερδευονται ακομα περισσοτερο γιατι δεν εμποδιζει τιποτα την

να υπακουει αλλου την πρωτη και αλλου τη δευτερη συνθηκη, 'πηδωντας' απο τη μια ακεραια τιμη του

στην αλλη.
Ακριβώς. Γι αυτό ήμουν προσεκτικός στο αρχικό μήνυμα (στην λύση μου της μη περιοδικότητας της

) να γράψω ότι το k
και το πρόσημο + ή - εξαρτώνται από το x.
Συμπέρασμα: Φαίνεται ότι το πρόβλημα έχει ενδιαφέρον.
Τελικά υπάρχουν και πιο περίεργες συνεχείς συναρτήσεις οι οποίες πηδάνε από + σε -. Θα περιγράψω μια τέτοια πάρακάτω
Στο [0,1] η g θα παίρνει την τιμή

, για κάποιο ακέραιο

Στο [2,3] η g θα παίρνει την τιμή

, για κάποιο ακέραιο

Στο [-2,-1] η g θα παίρνει την τιμή

, για κάποιο ακέραιο

κτλ
Πιο συγκεκριμένα στο [2κ,2κ+1] η g θα παίρνει την τιμή

, για κάποιο ακέραιο

Στα [-1,0],[1,2] κτλ η g θα είναι γραμμική.
Σίγουρα η g είναι συνεχής και έχω ελεύθερη επιλογή για να διαλέξω τα

.
Νέος περιορισμός: Για κάθε κ, θα ισχύει

Για αυτή την συνάρτηση g, η

είναι περιοδική με περίοδο 2. Πράγματι αν
![x \in \bigcup_{k \in \mathbb{Z}} [2k,2k+1] x \in \bigcup_{k \in \mathbb{Z}} [2k,2k+1]](/forum/ext/geomar/texintegr/latexrender/pictures/1b043ac796aef8103d38e46b54e609e2.png)
τότε έχουμε

Αν
![x \in [2k+1,2k+2] x \in [2k+1,2k+2]](/forum/ext/geomar/texintegr/latexrender/pictures/89af3e4d39ac9670896d99ea02eaf897.png)
με

τότε έχουμε

και αν
![x \in [2k+1,2k+2] x \in [2k+1,2k+2]](/forum/ext/geomar/texintegr/latexrender/pictures/89af3e4d39ac9670896d99ea02eaf897.png)
με

τότε έχουμε

.
(Κάντε ένα σχήμα.)
Μένει να δείξω πως μπορώ να διαλέξω τα

ώστε η g να μην είναι της μορφής που περιγράφει ο Δημήτρης (dement). Ένας τρόπος είναι να τα διαλέξω ως εξής

όπου στα αριστερά συνεχίζει περιοδικά και στα δεξία (εκεί όπου η g και δεν είναι της μορφής που περιγράφει ο Δημήτρης) ανεβαίνει 2 βήματα, καταβαίνει 3, ανεβαίνει 4, κτλ.

 .
.
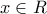 θα ισχύει
θα ισχύει 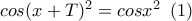
 άρα υπάρχει ακέραιος κ , ώστε
άρα υπάρχει ακέραιος κ , ώστε  (κ > 0) δηλαδή
(κ > 0) δηλαδή 

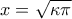 παίρνουμε
παίρνουμε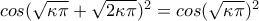

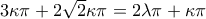 (3) ή
(3) ή  (4)
(4) ,άτοπο(άρρητος=ρητός)
,άτοπο(άρρητος=ρητός) άτοπο(άρρητος=ρητός)
άτοπο(άρρητος=ρητός) .
. (που εξαρτάται από το x) και κατάλληλο κάθε φορά πρόσημο + ή - με
(που εξαρτάται από το x) και κατάλληλο κάθε φορά πρόσημο + ή - με  . Αλλά τότε
. Αλλά τότε  . Αυτό όμως είναι άτοπο διότι οι
. Αυτό όμως είναι άτοπο διότι οι ,
, 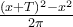 ως συνεχείς συναρτήσεις παίρνουν "όλες τις ενδιάμεσες τιμές": Από αυτό εύκολα βλέπουμε ότι υπάρχει κοινό διάστημα τιμών του x που ούτε η μία ούτε η άλλη δεν έχουν ακέραια τιμή.
ως συνεχείς συναρτήσεις παίρνουν "όλες τις ενδιάμεσες τιμές": Από αυτό εύκολα βλέπουμε ότι υπάρχει κοινό διάστημα τιμών του x που ούτε η μία ούτε η άλλη δεν έχουν ακέραια τιμή. και άλλες παρόμοιες.
και άλλες παρόμοιες.  περιοδικη με περιοδο
περιοδικη με περιοδο  . Τοτε, για καθε
. Τοτε, για καθε  , εχουμε
, εχουμε  η
η  με
με  .
.  ). Τοτε, αφου η
). Τοτε, αφου η  ειναι συνεχης και παιρνει ακεραιες τιμες, ειναι σταθερη. Απο αυτο επεται οτι η
ειναι συνεχης και παιρνει ακεραιες τιμες, ειναι σταθερη. Απο αυτο επεται οτι η  πρεπει να ειναι τετοια ωστε η
πρεπει να ειναι τετοια ωστε η  να ειναι περιοδικη με περιοδο
να ειναι περιοδικη με περιοδο  .
. ).
).  ) να γράψω ότι το k και το πρόσημο + ή - εξαρτώνται από το x.
) να γράψω ότι το k και το πρόσημο + ή - εξαρτώνται από το x.  , για κάποιο ακέραιο
, για κάποιο ακέραιο 
 , για κάποιο ακέραιο
, για κάποιο ακέραιο 
 , για κάποιο ακέραιο
, για κάποιο ακέραιο 
 , για κάποιο ακέραιο
, για κάποιο ακέραιο 
 .
.
 είναι περιοδική με περίοδο 2. Πράγματι αν
είναι περιοδική με περίοδο 2. Πράγματι αν ![x \in \bigcup_{k \in \mathbb{Z}} [2k,2k+1] x \in \bigcup_{k \in \mathbb{Z}} [2k,2k+1]](/forum/ext/geomar/texintegr/latexrender/pictures/1b043ac796aef8103d38e46b54e609e2.png) τότε έχουμε
τότε έχουμε  Αν
Αν ![x \in [2k+1,2k+2] x \in [2k+1,2k+2]](/forum/ext/geomar/texintegr/latexrender/pictures/89af3e4d39ac9670896d99ea02eaf897.png) με
με  τότε έχουμε
τότε έχουμε  τότε έχουμε
τότε έχουμε  .
.