 .
.Υ.Γ. Η άσκηση είναι για τους μεγάλους. Πρέπει να έχουν έναν καλό λόγο για να μείνουν στο σπίτι, γιατί στην ηλικία τους, δεν επιτρέπονται συγκινήσεις!
Συντονιστής: exdx
 .
..Ορέστης Λιγνός έγραψε: ↑Παρ Απρ 20, 2018 2:22 pmΝα υπολογιστεί η παράσταση.
Υ.Γ. Η άσκηση είναι για τους μεγάλους. Πρέπει να έχουν έναν καλό λόγο για να μείνουν στο σπίτι, γιατί στην ηλικία τους, δεν επιτρέπονται συγκινήσεις!Οι νεαροί, ραντεβού στο ΣΕΦ, μας χρειάζεται ο Θρύλος και ο Kill Bill!
 .
.
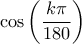 κάτω από τη ρίζα, μαζί με το
κάτω από τη ρίζα, μαζί με το  , είναι οι
, είναι οι  ρίζες του πολυωνύμου
ρίζες του πολυωνύμου  (ως προς
(ως προς  ). Χρησιμοποιώντας τον τύπο
). Χρησιμοποιώντας τον τύπο![\sin [(n+1)x] + \sin[(n-1)x] = 2 \cos x \sin (nx) \sin [(n+1)x] + \sin[(n-1)x] = 2 \cos x \sin (nx)](/forum/ext/geomar/texintegr/latexrender/pictures/20aa21faa5d14ffa1e8c5e3a1c0b16c1.png)
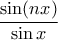 είναι πολυώνυμο βαθμού
είναι πολυώνυμο βαθμού  με μεγιστοβάθμιο συντελεστή
με μεγιστοβάθμιο συντελεστή  , σταθερό όρο
, σταθερό όρο  και πρωτοβάθμιο συντελεστή
και πρωτοβάθμιο συντελεστή  για
για  περιττό και
περιττό και  για
για  άρτιο.
άρτιο. .
.Ορέστης Λιγνός έγραψε: ↑Παρ Απρ 20, 2018 2:22 pmΝα υπολογιστεί η παράσταση.
Υ.Γ. Η άσκηση είναι για τους μεγάλους. Πρέπει να έχουν έναν καλό λόγο για να μείνουν στο σπίτι, γιατί στην ηλικία τους, δεν επιτρέπονται συγκινήσεις!Οι νεαροί, ραντεβού στο ΣΕΦ, μας χρειάζεται ο Θρύλος και ο Kill Bill!
Ευχαριστώ τον nikkru και τον Δημήτρη για τις απαντήσεις τους!ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Σάβ Απρ 21, 2018 10:46 amΟρέστης Λιγνός έγραψε: ↑Παρ Απρ 20, 2018 2:22 pmΝα υπολογιστεί η παράσταση.
Υ.Γ. Η άσκηση είναι για τους μεγάλους. Πρέπει να έχουν έναν καλό λόγο για να μείνουν στο σπίτι, γιατί στην ηλικία τους, δεν επιτρέπονται συγκινήσεις!Οι νεαροί, ραντεβού στο ΣΕΦ, μας χρειάζεται ο Θρύλος και ο Kill Bill!
Γεια σου Ορέστη.
Δεν ξέρω που την ξέθαψες αλλά είναι μέρος της άσκησης 4 σελ 194 στην
ΤΡΙΓΩΝΟΜΕΤΡΙΑ 1 του Ι.ΜΑΝΤΑ.
Πρέπει να υπάρχει και σε άλλα ''παλιά'' βιβλία Τριγωνομετρίας.


 , κλπ...
, κλπ... .
.  και λύνοντας πρώτα ως προς
και λύνοντας πρώτα ως προς 

 παίρνουμε
παίρνουμε 




 .
. είναι
είναι  (αφού
(αφού  )
) .
.  γίνεται με τη βοήθεια του τύπου
γίνεται με τη βοήθεια του τύπου  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες