Αν είναι
 τότε να βρεθεί η μέγιστη τιμή των
τότε να βρεθεί η μέγιστη τιμή των  και
και 
Το θέμα έχει πιθανότατα καλυφθεί. Θα πρότεινα οι παραπομπές σε λύσεις να καθυστερήσουν λίγο ,
ώστε να δούμε πρώτα κάποιες απαντήσεις και ( γιατί όχι) νέες ιδέες-λύσεις! .
Σας ευχαριστώ , Γιώργος.
Συντονιστής: exdx
 τότε να βρεθεί η μέγιστη τιμή των
τότε να βρεθεί η μέγιστη τιμή των  και
και 
 με το μέγιστο, που είναι
με το μέγιστο, που είναι  , να επιτυγχάνεται όταν
, να επιτυγχάνεται όταν  , που, για
, που, για  , προκύπτει όταν
, προκύπτει όταν  .
. με το μέγιστο, που είναι
με το μέγιστο, που είναι  ,να επιτυγχάνεται όταν
,να επιτυγχάνεται όταν  , που, για
, που, για  προκύπτει όταν
προκύπτει όταν  .
. σημείο στο 1ο τεταρτοκύκλιο του μοναδιαίου κύκλου.
σημείο στο 1ο τεταρτοκύκλιο του μοναδιαίου κύκλου. .
. , άρα και του
, άρα και του  επιτυγχάνεται όταν
επιτυγχάνεται όταν  .
. .
. επιτυγχάνεται όταν
επιτυγχάνεται όταν  .
. είναι ορθογώνιο τρίγωνο με
είναι ορθογώνιο τρίγωνο με  ●
● 
 δηλαδή
δηλαδή 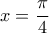
 με την ισότητα να ισχύει όταν
με την ισότητα να ισχύει όταν  δηλαδή
δηλαδή 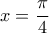
 σε ορθογώνιο τρίγωνο
σε ορθογώνιο τρίγωνο  με υποτείνουσα
με υποτείνουσα  ,
,  ύψος στην υποτείνουσα και
ύψος στην υποτείνουσα και  διάμεσο στην υποτείνουσα.
διάμεσο στην υποτείνουσα. , με το ίσον όταν το ύψος ταυτίζεται με τη διάμεσο, δηλαδή όταν είναι ισοσκελές.
, με το ίσον όταν το ύψος ταυτίζεται με τη διάμεσο, δηλαδή όταν είναι ισοσκελές.  .
. . Όταν το
. Όταν το  γίνεται μέγιστο, τότε γίνεται μέγιστο και το
γίνεται μέγιστο, τότε γίνεται μέγιστο και το 
 , άρα και το
, άρα και το  με μέγιστη τιμή
με μέγιστη τιμή  .
.
 .
.  .
. για
για  ,
,  ,
,  για
για  , άρα έχει μέγιστο όταν
, άρα έχει μέγιστο όταν  με τιμή
με τιμή  .
.
 .
.  με τιμή
με τιμή  .
. διχοτομεί την
διχοτομεί την  και το τετράγωνο
και το τετράγωνο  έχει πλευρά ίση με
έχει πλευρά ίση με  .
.  με
με  (όμοια η απόδειξη για
(όμοια η απόδειξη για  )
)  αφού :
αφού : η
η  είναι εγγεγραμμένη στο τόξο
είναι εγγεγραμμένη στο τόξο  που είναι μικρότερο του τεταρτοκυκλίου άρα
που είναι μικρότερο του τεταρτοκυκλίου άρα  δηλ
δηλ  .
.  όταν
όταν  .
. άρα
άρα 
 όταν
όταν  για
για  . Φιλικά Γιώργος.
. Φιλικά Γιώργος. ισχύει :
ισχύει : 
 .
.  στο
στο ![\left [ 0,\frac{\pi }{2} \right ] \left [ 0,\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/e91276fd1f8caf39b0cda9b60deb1b07.png) είναι
είναι  που συμβαίνει όταν
που συμβαίνει όταν  δηλαδή για
δηλαδή για  . ( Από τη σχέση
. ( Από τη σχέση  συμπεραίνουμε ότι, όταν η
συμπεραίνουμε ότι, όταν η  παρουσιάζει μέγιστο ή ελάχιστο στο
παρουσιάζει μέγιστο ή ελάχιστο στο  είναι
είναι  )
) η : Όταν το άθροισμα των τετραγώνων δύο αριθμών είναι σταθερό το άθροισμά τους
η : Όταν το άθροισμα των τετραγώνων δύο αριθμών είναι σταθερό το άθροισμά τους η : Όταν το άθροισμα των τετραγώνων δύο αριθμών είναι σταθερό το γινόμενό τους
η : Όταν το άθροισμα των τετραγώνων δύο αριθμών είναι σταθερό το γινόμενό τους και
και 
 , για τα μέγιστα παίρνουμε :
, για τα μέγιστα παίρνουμε :  και
και  , αμφότερα για :
, αμφότερα για :  , δηλαδή για
, δηλαδή για  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες