τετραγώνων τριών διαδοχικών όρων να ισούται με το
Συντονιστής: exdx
Δεν έχω σβέλτη λύση, αλλά ας είναι. Κάνω μία μακροσκελή.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τρί Δεκ 19, 2023 11:13 pmΝα αποδείξετε ότι δεν υπάρχει αριθμητική πρόοδος με όρους φυσικούς αριθμούς, της οποίας το άθροισμα των
τετραγώνων τριών διαδοχικών όρων να ισούται με το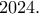
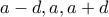 , και θέλουμε να ισχύει
, και θέλουμε να ισχύει 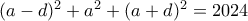 , ισοδύναμα
, ισοδύναμα 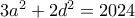 .
.  άρτιος, έστω
άρτιος, έστω  . Άρα η εξίσωση γίνεται
. Άρα η εξίσωση γίνεται 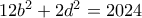 , ισοδύναμα
, ισοδύναμα  . Άρα
. Άρα  άρτιος, έστω
άρτιος, έστω  , και η εξίσωση γίνεται
, και η εξίσωση γίνεται 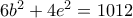 , ισοδύναμα
, ισοδύναμα 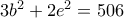 . Άρα
. Άρα  άρτιος, έστω
άρτιος, έστω 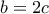 , και η εξίσωση γίνεται
, και η εξίσωση γίνεται 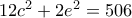 , ισοδύναμα
, ισοδύναμα 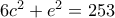 .
. περιττός και επιπλέον, επειδή το
περιττός και επιπλέον, επειδή το  δεν είναι πολλαπλάσιο του
δεν είναι πολλαπλάσιο του  , έπεται ότι ούτε το
, έπεται ότι ούτε το  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  . Τα δύο μαζί δίνουν ότι
. Τα δύο μαζί δίνουν ότι 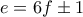 , οπότε η σχέση γράφεται
, οπότε η σχέση γράφεται 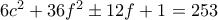 , ισοδύναμα
, ισοδύναμα 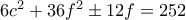 και άρα
και άρα 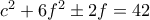 . Συνεπώς
. Συνεπώς  άρτιος, έστω
άρτιος, έστω 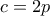 , οπότε
, οπότε 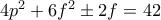 και άρα
και άρα 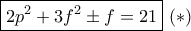 .
. 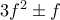 είναι άρτιος αριθμός ό,τι και αν είναι το
είναι άρτιος αριθμός ό,τι και αν είναι το  (πράγματι, αυτό είναι άμεσο αν
(πράγματι, αυτό είναι άμεσο αν  άρτιος ενώ αν
άρτιος ενώ αν  περιττός τότε πάλι ο
περιττός τότε πάλι ο 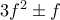 είναι άρτιος ως άθροισμα δύο περιττών.)
είναι άρτιος ως άθροισμα δύο περιττών.) είναι άρτιος αριθμός. Άτοπο αφού το δεξί μέλος είναι περιττός. Τελικά, δεν υπάρχουν ακέραιοι αριθμοί που ικανοποιούν την αρχική συνθήκη, όπως θέλαμε να δείξουμε.
είναι άρτιος αριθμός. Άτοπο αφού το δεξί μέλος είναι περιττός. Τελικά, δεν υπάρχουν ακέραιοι αριθμοί που ικανοποιούν την αρχική συνθήκη, όπως θέλαμε να δείξουμε.Mihalis_Lambrou έγραψε: ↑Σάβ Δεκ 30, 2023 9:51 pmΔεν έχω σβέλτη λύση, αλλά ας είναι. Κάνω μία μακροσκελή.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τρί Δεκ 19, 2023 11:13 pmΝα αποδείξετε ότι δεν υπάρχει αριθμητική πρόοδος με όρους φυσικούς αριθμούς, της οποίας το άθροισμα των
τετραγώνων τριών διαδοχικών όρων να ισούται με το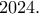
Η αριθμητική πρόοδος είναι της μορφής, και θέλουμε να ισχύει
, ισοδύναμα
.
Έπεται ότιάρτιος, έστω
. Άρα η εξίσωση γίνεται
, ισοδύναμα
. Άρα
άρτιος, έστω
, και η εξίσωση γίνεται
, ισοδύναμα
. Άρα
άρτιος, έστω
, και η εξίσωση γίνεται
, ισοδύναμα
.
ΚΑΛΗ ΧΡΟΝΙΑ Μιχάλη.
Μέχρι εδώ, έχω την ίδια λύση.
Στη συνέχεια, εκτός τον τρόπο που παίρνουμε περιπτώσεις για το, θα μπορούσε κάποιος να το δει και ως εξής:
Αν, τότε
, άτοπο. Άρα
. Τότε ο
λήγει σε
αντιστοίχως.
Άρα oλήγει σε
. Άρα ο
λήγει σε
αντιστοίχως.
Για να είναι όμως οτέλειο τετράγωνο, όπως το θέλουμε, θα πρέπει (όχι βέβαια και αρκεί) να λήγει σε
Άρα, ή
. Με
έχουμε
, που δεν είναι τέλειο τετράγωνο. Όμοια και αν
Άρα δείξαμε το ζητούμενο.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες