 με ύψος
με ύψος  , ισχύει
, ισχύει 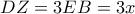 . Επί του
. Επί του  παίρνω σημείο
παίρνω σημείο  με
με  και φέρω
και φέρω  και
και  . Αν
. Αν  , βρείτε το λόγο
, βρείτε το λόγο  .
.Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 με ύψος
με ύψος  , ισχύει
, ισχύει 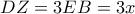 . Επί του
. Επί του  παίρνω σημείο
παίρνω σημείο  με
με  και φέρω
και φέρω  και
και  . Αν
. Αν  , βρείτε το λόγο
, βρείτε το λόγο  .
. παίρνουμε σημείο
παίρνουμε σημείο  , ώστε
, ώστε  και από το
και από το  φέρνουμε παράλληλη προς την
φέρνουμε παράλληλη προς την  , η οποία τέμνει την
, η οποία τέμνει την  στο
στο  και την
και την  στο
στο  , οπότε είναι
, οπότε είναι  ,
,  ,
,  ,
,  και το
και το  είναι παραλληλόγραμμο με
είναι παραλληλόγραμμο με  .
.
 έχουμε :
έχουμε : 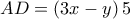 και από την προηγούμενη σχέση παίρνουμε
και από την προηγούμενη σχέση παίρνουμε  .
.  .
.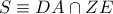 ,
,  ,
,  και
και  . Είναι
. Είναι  (από το ισοσκελές τραπέζιο)
(από το ισοσκελές τραπέζιο)  (απ’ τα εγγράψιμα τετράπλευρα
(απ’ τα εγγράψιμα τετράπλευρα  )
)  (
( ).
). έχουμε:
έχουμε: 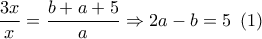 . Απ’ το λόγο ομοιότητας των τριγώνων
. Απ’ το λόγο ομοιότητας των τριγώνων  έχουμε:
έχουμε:  .
. παίρνουμε
παίρνουμε  και απ’ το λόγο ομοιότητας των τριγώνων
και απ’ το λόγο ομοιότητας των τριγώνων  :
:  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες