Σελίδα 1 από 1
Σπαζοκεφαλιά με εμβαδά
Δημοσιεύτηκε: Τετ Μάιος 08, 2013 2:59 pm
από KARKAR

- Σπαζοκεφαλιά με εμβαδά.png (11.92 KiB) Προβλήθηκε 385 φορές
Στην πλευρά

του τριγώνου

, βρίσκεται σταθερό σημείο

, ώστε

.
Σημείο

κινείται επί της

, ενώ

και

τέμνονται στο σημείο

.
1) Για ποια θέση του

είναι

?
2) Μπορεί να βρεθεί τύπος , που να δίνει το

, συναρτήσει του λόγου

?
Re: Σπαζοκεφαλιά με εμβαδά
Δημοσιεύτηκε: Τετ Μάιος 08, 2013 6:52 pm
από KDORTSI

- Συσχέτιση εμβαδών.PNG (24.6 KiB) Προβλήθηκε 322 φορές
Θα βρούμε πρώτα το γενικό τύπο του δευτέρου ερωτήματος κι΄υστερα ως εφαρμογή το πρώτο ερώτημα.
Από το θεώρημα του Μενελάου στο τρίγωνο

με διατέμνουσα την

προκύπτει:

και με τα δεδομένα του προβλήματος και του σχήματος συμπεραίνεται:

Ακόμα από το σχήμα φαίνεται:

και επειδή τα τρίγωνα
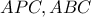
έχουν το ίδιο ύψος, ο λόγος των εμβαδών είναι ίσος με το λόγο των βάσεων, δηλαδή

η τελευταία σχέση γίνεται:

Επίσης είναι:

Η σχέση (2) σύμφωνα με την (3) και την (1) δίνει:

και αν θέσουμε:

τότε η τελευταία γίνεται:

η σχέση αυτή δίνει τη σχέση των εμβαδών αυτών συναρτήσει του μερικού λόγου
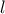
που ορίζει το σημείο

με τις κορυφές

.
Αν θέλουμε τώρα να είναι

τότε από τη σχέση που βρήκαμε κάνοντας πράξεις και λύνοντας μια δευτεροβάθμια εξίσωση
βρίσκουμε ότι:
 Παρατήρηση: Το ανωτέρω σχήμα έγινε σύμφωνα με την τιμή αυτή και επαληθεύτηκε η ορθότητα της απάντησης.
Παρατήρηση: Το ανωτέρω σχήμα έγινε σύμφωνα με την τιμή αυτή και επαληθεύτηκε η ορθότητα της απάντησης.
Κώστας Δόρτσιος
Re: Σπαζοκεφαλιά με εμβαδά
Δημοσιεύτηκε: Τετ Μάιος 08, 2013 7:33 pm
από Γιώργος Ρίζος
Στα χνάρια του Κώστα Δόρτσιου, με μία διαφορά:
Ο πεπειραμένος γεωμέτρης ξεκινά (άνετα) από τη γενίκευση και κατόπιν εφαρμόζει τον τύπο για όποια τιμή θέλει.
Ο άπειρος ασκούμενος ξεκινά (κατά POLYA) από την ειδική περίπτωση και κατόπιν γενικεύει....

- Σπαζοκεφαλιά με εμβαδά.png (11.92 KiB) Προβλήθηκε 295 φορές
Είναι

Έστω

, οπότε

Από Θ. Μενελάου στο

είναι

,
δηλαδή

Οπότε

Άρα

Οπότε

Γενικεύοντας,

Έστω

Είναι
 edit:
edit: Πρόσθεσα τη γενίκευση στις 20:12
Re: Σπαζοκεφαλιά με εμβαδά
Δημοσιεύτηκε: Πέμ Μάιος 09, 2013 2:11 am
από Μιχάλης Τσουρακάκης
Καλημέρα. Μια ακόμη αντιμετώπιση χωρίς Μενέλαο.
Έστω


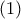
Ακόμη ,

Από (1),(2) παίρνουμε εύκολα


.


και βάσει της (3) έχουμε

, οπότε,


Στην ειδική περίπτωση που

,λύνοντας την δευτεροβάθμια εξίσωση

στην οποία καταλήγουμε παίρνουμε,

 του τριγώνου
του τριγώνου  , βρίσκεται σταθερό σημείο
, βρίσκεται σταθερό σημείο  , ώστε
, ώστε  .
.  κινείται επί της
κινείται επί της  , ενώ
, ενώ  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  .
. είναι
είναι  ?
? , συναρτήσει του λόγου
, συναρτήσει του λόγου  ?
? του τριγώνου
του τριγώνου  , βρίσκεται σταθερό σημείο
, βρίσκεται σταθερό σημείο  , ώστε
, ώστε  .
.  κινείται επί της
κινείται επί της  , ενώ
, ενώ  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  .
. είναι
είναι  ?
? , συναρτήσει του λόγου
, συναρτήσει του λόγου  ?
? με διατέμνουσα την
με διατέμνουσα την  προκύπτει:
προκύπτει: 


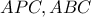 έχουν το ίδιο ύψος, ο λόγος των εμβαδών είναι ίσος με το λόγο των βάσεων, δηλαδή
έχουν το ίδιο ύψος, ο λόγος των εμβαδών είναι ίσος με το λόγο των βάσεων, δηλαδή 



 τότε η τελευταία γίνεται:
τότε η τελευταία γίνεται: 
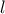 που ορίζει το σημείο
που ορίζει το σημείο  με τις κορυφές
με τις κορυφές  .
. τότε από τη σχέση που βρήκαμε κάνοντας πράξεις και λύνοντας μια δευτεροβάθμια εξίσωση
τότε από τη σχέση που βρήκαμε κάνοντας πράξεις και λύνοντας μια δευτεροβάθμια εξίσωση 

 , οπότε
, οπότε 
 είναι
είναι  ,
,



 Έστω
Έστω 



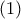


 .
.
 και βάσει της (3) έχουμε
και βάσει της (3) έχουμε  , οπότε,
, οπότε, 

 ,λύνοντας την δευτεροβάθμια εξίσωση
,λύνοντας την δευτεροβάθμια εξίσωση  στην οποία καταλήγουμε παίρνουμε,
στην οποία καταλήγουμε παίρνουμε, 