 διαμέτρου
διαμέτρου  και χορδή του
και χορδή του 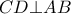 . Στο ημικύκλιο που βρίσκεται το
. Στο ημικύκλιο που βρίσκεται το  κινείται σημείο
κινείται σημείο  .
.Η
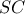 τέμνει την ευθεία
τέμνει την ευθεία  στο
στο  και η
και η  στο
στο  . Το ημικύκλιο διαμέτρου
. Το ημικύκλιο διαμέτρου  τέμνει τον κύκλο
τέμνει τον κύκλο  στο
στο  . Να δειχθεί ότι
. Να δειχθεί ότι 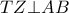 .
.Νίκος
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 διαμέτρου
διαμέτρου  και χορδή του
και χορδή του 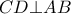 . Στο ημικύκλιο που βρίσκεται το
. Στο ημικύκλιο που βρίσκεται το  κινείται σημείο
κινείται σημείο  .
.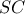 τέμνει την ευθεία
τέμνει την ευθεία  στο
στο  και η
και η  στο
στο  . Το ημικύκλιο διαμέτρου
. Το ημικύκλιο διαμέτρου  τέμνει τον κύκλο
τέμνει τον κύκλο  στο
στο  . Να δειχθεί ότι
. Να δειχθεί ότι 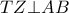 .
.ΜεDoloros έγραψε: Έστω κύκλοςδιαμέτρου
και χορδή του
. Στο ημικύκλιο που βρίσκεται το
κινείται σημείο
.
Ητέμνει την ευθεία
στο
και η
στο
. Το ημικύκλιο διαμέτρου
τέμνει τον κύκλο
στο
. Να δειχθεί ότι
.
Νίκος
 κάθετη στη διάμετρο του
κάθετη στη διάμετρο του  αρμονική οπότε και η σειρά
αρμονική οπότε και η σειρά 
 είναι αρμονική και με
είναι αρμονική και με  διχοτόμο της γωνίας
διχοτόμο της γωνίας  .
. (από τη διάμετρο
(από τη διάμετρο  του "νέου" ημικυκλίου ) προκύπτει ότι
του "νέου" ημικυκλίου ) προκύπτει ότι 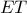 εφαπτόμενη του
εφαπτόμενη του 
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. που τέμνει τον κύκλο στο
που τέμνει τον κύκλο στο  οπότε
οπότε  .Έστω ακόμη
.Έστω ακόμη  .Επειδή ,
.Επειδή ,  το
το  είναι ορθογώνιο κι επομένως
είναι ορθογώνιο κι επομένως 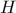 μέσον της
μέσον της  και η
και η  είναι μεσοκάθετος της
είναι μεσοκάθετος της  άρα
άρα 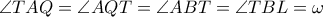 (γιατί το
(γιατί το  είναι εγγράψιμο)και
είναι εγγράψιμο)και 
 θα είναι
θα είναι  διχοτόμος της
διχοτόμος της  κι αφού
κι αφού  εξωτερική διχοτόμος του τριγώνου
εξωτερική διχοτόμος του τριγώνου  .Άρα
.Άρα
 είναι συνευθειακά και γι αυτό είναι αρκετό να αποδείξουμε ότι
είναι συνευθειακά και γι αυτό είναι αρκετό να αποδείξουμε ότι  κι επειδή από την
κι επειδή από την 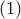
 αρκεί να αποδείξουμε ότι
αρκεί να αποδείξουμε ότι .Η τελευταία όμως είναι αληθής αφού
.Η τελευταία όμως είναι αληθής αφού  ..
..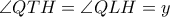 .Όμως ,
.Όμως ,  κι αφού το τρίγωνο
κι αφού το τρίγωνο  είναι ορθογώνιο,θα είναι
είναι ορθογώνιο,θα είναι  εγγράψιμο ,άρα
εγγράψιμο ,άρα  και το ζητούμενο αποδείχτηκε
και το ζητούμενο αποδείχτηκε είναι συμμετρικά ως προς τη διάμετρο. Είναι
είναι συμμετρικά ως προς τη διάμετρο. Είναι  , άρα αφού
, άρα αφού  τα τρίγωνα
τα τρίγωνα  και
και  είναι όμοια οπότε:
είναι όμοια οπότε: , άρα το
, άρα το  ανήκει στο ριζικό άξονα των δύο κύκλων όπως προφανώς και το
ανήκει στο ριζικό άξονα των δύο κύκλων όπως προφανώς και το  , οπότε η ευθεία
, οπότε η ευθεία  ως ριζικός άξονας είναι κάθετη στη διάκεντρο.
ως ριζικός άξονας είναι κάθετη στη διάκεντρο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες