Τα προς τρίτον τινί ίσα και αλλήλοις ίσα

[Doloros]

τα πρός τρίτον ίσα και αλλήλοις ίσα.png (14.77 KiB) Προβλήθηκε 553 φορές

Δίδεται σκαληνό τρίγωνο και πάνω στα ύψη του θεωρούμε αντίστοιχα τα σημεία για τα οποία .

Γράφουμε τους περιγεγραμμένους κύκλους των τριγώνων και έστω ένα από τα κοινά τους σημεία .

Δείξετε ότι η διχοτομεί τη γωνία .

[rek2]

Λόγω κακής σύνδεσης, βάζω μία ισχυρή υπόδειξη μόνο:

Αν η τέμνει την στο και οι δύο κύκλοι επανατέμνουν την , στα (ο μπλε) και (ο κόκκινος) τότε το έχει ίσες δυνάμεις ως προς τους δύο κύκλους. Η σχέση



λόγω των ισοτήτων και θα δώσει μετά τις πράξεις

κ.λπ. το ανήκει στην διχοτόμο.

Υ.Γ. Νίκο, δεν πρέπει να υπάρχει συμφωνία κατά γένος, αριθμό και πτώση;

[giannimani]

exer15png_Page1.png (49.4 KiB) Προβλήθηκε 373 φορές

Έστω ο περίκυκλος του τριγώνου (κέντρου μέσου του ), ο περίκυκλος του τριγώνου (κέντρου μέσου του ), και 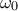ο κύκλος που διέρχεται από τα σημεία , , , (κέντρου μέσου του ). Έστω επίσης , τα σημεία τομής των κύκλων , . Τότε οι ευθείες των κοινών χορδών των κύκλων 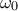, , (που τέμνονται ανά δύο) διέρχονται από το ίδιο σημείο (ριζικό κέντρο των τριών κύκλων) ή είναι παράλληλες. Εφόσον, όμως οι ευθείες και των κοινών χορδών των κύκλων 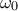, και 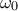, διέρχονται από το σημείο , τότε και η ευθεία της κοινής χορδής των , θα διέρχεται επίσης από το .

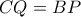Έστω, τώρα το μέσο του , και το συμμετρικό του ως προς το μέσο του . Λόγω της υπόθεσης () και της συμμετρίας ως προς το σημείο , το τρίγωνο είναι ισοσκελές (). Εύκολα αποδεικνύεται ότι το τετράπλευρο είναι ρόμβος, οπότε οι διαγώνιοί του και τέμνονται κάθετα, και 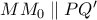. Εφόσον η κοινή χορδή των κύκλων , είναι κάθετος στη διάκεντρό τους , τότε .

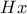Στη συνέχεια, έστω ( το ορθόκεντρο του τριγώνου ) η διχοτόμος της γωνίας . Θα αποδείξουμε ότι . Είναι . Επομένως, .
Επίσης .
Από τα παραπάνω προκύπτει ότι .
Απομένει να αποδείξουμε ότι οι διχοτόμοι των γωνιών και είναι παράλληλοι. Αυτό προκύπτει εύκολα εφόσον στον κύκλο τα σημεία και (μέσα των τόξων και αντίστοιχα) είναι αντιδιαμετρικά σημεία του, οπότε το τετράπλευρο είναι ορθογώνιο,

[Doloros]

Καλησπέρα.
Ευχαριστώ τους Κώστα και Γιάννη για τις λύσεις τους

Η δική μου πολύ κοντά σ αυτή του Γιάννη .

Τα πρός τρίτον ίσα και αλλήλοις ίσα_λύση.png (22.15 KiB) Προβλήθηκε 365 φορές

Επειδή τα σημεία ανήκουν στον ίδιο κύκλο το σημείο είναι το ριζικό κέντρο των τριών κύκλων : .

Ο κύκλος έχει διάμετρο κέντρο το μέσο του , το οποίο ανήκει ακόμα στη μεσοκάθετο του που διέρχεται από μέσο του

Κι αυτό γιατί .

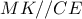Από το όμως θα διέρχεται και η μεσοκάθετος του γιατί ( διάμεσοι ορθογωνίων τριγώνων προς κοινή υποτείνουσα).

Στο τρίγωνο το ευθύγραμμο τμήμα συνδέει τα μέσα δύο πλευρών του και άρα , ομοίως δε .

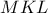Οι δύο προηγούμενες μας εξασφαλίζουν ότι το τρίγωνο είναι ισοσκελές . Θα είναι ( κάθετες πλευρές αφού ) .

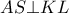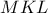Δηλαδή κάθε μια από τις ίσες γωνίες του ισοσκελούς τριγώνου , ισούται με κάθε μια από τις δύο γωνίες που χωρίζεται η από την .

Νίκος

Η άσκηση όπως με είχε ενημερώσει πριν 2-3 μέρες ο είχε πάλι ανεβεί και πιο παλιά εδώ ( ξεχνάω πολύ )