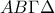 με την διαγώνιό του
με την διαγώνιό του 
να είναι διάμετρος του κύκλου. Αν
 ,
,  και
και , να δείξετε ότι το
, να δείξετε ότι το  είναι μέσο της
είναι μέσο της  .
.Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
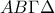 με την διαγώνιό του
με την διαγώνιό του 
 ,
,  και
και , να δείξετε ότι το
, να δείξετε ότι το  είναι μέσο της
είναι μέσο της  .
.
 , οπότε
, οπότε  , ό. έ. δ.
, ό. έ. δ.Καλημέρα. Από Π.Θ:Φανης Θεοφανιδης έγραψε:
Δίνεται το εγγεγραμμένο τετράπλευρομε την διαγώνιό του

να είναι διάμετρος του κύκλου. Αν,
και
, να δείξετε ότι το
είναι μέσο της
.




Καλημέρα σε όλους!Φανης Θεοφανιδης έγραψε:444.png
Δίνεται το εγγεγραμμένο τετράπλευρομε την διαγώνιό του

να είναι διάμετρος του κύκλου. Αν,
και
, να δείξετε ότι το
είναι μέσο της
.
 Από Π. Θ στα
Από Π. Θ στα 




Για μια καλημέρα στους εκλεκτούς φίλους (από τις μακρυνές Βρυξέλλες) που "φυλάνε Θερμοπύλες" στοΦανης Θεοφανιδης έγραψε: Δίνεται το εγγεγραμμένο τετράπλευρομε την διαγώνιό του
να είναι διάμετρος του κύκλου. Αν
,
και
, να δείξετε ότι το
είναι μέσο της
.
 είναι οι ορθές προβολές των
είναι οι ορθές προβολές των  στην
στην  αντίστοιχα , τότε από τα ορθογώνια τρίγωνα
αντίστοιχα , τότε από τα ορθογώνια τρίγωνα  το μέσο της
το μέσο της  και με
και με  (κάθετες στην ίδια ευθεία) θα είναι
(κάθετες στην ίδια ευθεία) θα είναι  το μέσο της
το μέσο της 


 το μέσο της
το μέσο της  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. και κέντρου
και κέντρου  θεωρώ σημείο
θεωρώ σημείο  τέτοιο ώστε:
τέτοιο ώστε:  . Αν
. Αν  το μέσο του
το μέσο του  και η ευθεία
και η ευθεία  τέμνει , ακόμα, το ημικύκλιο
τέμνει , ακόμα, το ημικύκλιο  , είναι φανερό ότι τα τρίγωνα
, είναι φανερό ότι τα τρίγωνα  είναι ισοσκελή ορθογώνια .
είναι ισοσκελή ορθογώνια . το μέσο του
το μέσο του 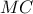 τα ορθογώνια τρίγωνα
τα ορθογώνια τρίγωνα  έχουν
έχουν και τις οξείες γωνίες τους στο
και τις οξείες γωνίες τους στο  ίσες ( από
ίσες ( από 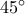 ) και θα είναι ίσα οπότε :
) και θα είναι ίσα οπότε : με άμεση συνέπεια ,
με άμεση συνέπεια , 
 το αντιδιαμετρικό του
το αντιδιαμετρικό του  .
. τέμνονται στο
τέμνονται στο  τα ορθογώνια τρίγωνα
τα ορθογώνια τρίγωνα  είναι
είναι  , Επειδή δε
, Επειδή δε  και το
και το  μέσο του
μέσο του  θα είναι και
θα είναι και  μέσο του
μέσο του  , δηλαδή
, δηλαδή  .
. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες