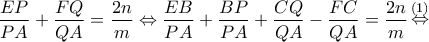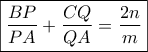σημείο της διαμέσου
σημείο της διαμέσου  , τριγώνου
, τριγώνου  , που τη διαιρεί σε λόγο
, που τη διαιρεί σε λόγο  .
.Δείξτε ότι για οποιαδήποτε τέμνουσα διερχόμενη από το
 και έχουσα τα άκρα της
και έχουσα τα άκρα της  στις πλευρές
στις πλευρές  αντίστοιχα, ισχύει :
αντίστοιχα, ισχύει : 
Παρατηρήσεις :
α. Η παρούσα αποτελεί γενίκευση παλιότερης άσκησης του Θανάση (KARKAR) και μπορεί να φανεί χρήσιμη, σαν λήμμα, στην λύση άλλων ασκήσεων.
β. Επειδή τα
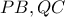 είναι στον αριθμητή μπορεί να χρησιμοποιηθεί και για τέμνουσες που διέρχονται από τα
είναι στον αριθμητή μπορεί να χρησιμοποιηθεί και για τέμνουσες που διέρχονται από τα  ή
ή 
γ. Ενα παράδειγμα εφαρμογής είναι αυτή

 παράλληλη στην
παράλληλη στην  που τέμνει τις
που τέμνει τις  αντίστοιχα και έστω
αντίστοιχα και έστω 
 και από τα όμοια τρίγωνα
και από τα όμοια τρίγωνα  είναι:
είναι: