 του σχήματος είναι
του σχήματος είναι  . Θεωρούμε τα
. Θεωρούμε τα 
ώστε να είναι
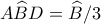 και
και  .
.Οι
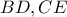 τέμνονται στο
τέμνονται στο  και έστω
και έστω  το έγκεντρο του τριγώνου
το έγκεντρο του τριγώνου  .
. Ο κύκλος
 τέμνει τις προεκτάσεις των
τέμνει τις προεκτάσεις των  στα
στα  αντίστοιχα .
αντίστοιχα .1) Να δειχθεί ότι τα τρίγωνα
 είναι ισόπλευρα κι' ακόμη ότι
είναι ισόπλευρα κι' ακόμη ότι  .
.Αν επιπλέον είναι
 τότε : 2) Να εξεταστεί αν ισχύει
τότε : 2) Να εξεταστεί αν ισχύει  .
.Ευχαριστώ , Γιώργος

 .
. , οπότε
, οπότε  ισόπλευρο.
ισόπλευρο. , και αφού
, και αφού  , η
, η  είναι η μεσοκάθετος της
είναι η μεσοκάθετος της  , και όμοια
, και όμοια  , επομένως και το
, επομένως και το  είναι ισόπλευρο.
είναι ισόπλευρο. παίρνουμε
παίρνουμε  , και άρα
, και άρα  .
.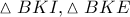 και εξισώνοντας θα πάρουμε
και εξισώνοντας θα πάρουμε  , επομένως
, επομένως  ή
ή 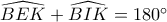 .
. , άτοπο.
, άτοπο.
 .
. .
. , και αφού
, και αφού  ,
,  .
.