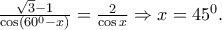Εύρεση γωνίας 2
Δημοσιεύτηκε: Πέμ Νοέμ 16, 2017 7:45 am
Στο παραπάνω σχήμα, να βρείτε τη γωνία  . Υπάρχουν λύσεις και για "μικρότερο" φάκελο!
. Υπάρχουν λύσεις και για "μικρότερο" φάκελο!
 . Υπάρχουν λύσεις και για "μικρότερο" φάκελο!
. Υπάρχουν λύσεις και για "μικρότερο" φάκελο! . Υπάρχουν λύσεις και για "μικρότερο" φάκελο!
. Υπάρχουν λύσεις και για "μικρότερο" φάκελο!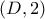 προς τη μεριά του
προς τη μεριά του  . Το αντιδιαμετρικό του
. Το αντιδιαμετρικό του  έστω
έστω  και
και  η ακτίνα που περνάει από το
η ακτίνα που περνάει από το  .
.  είναι ισόπλευρο και το
είναι ισόπλευρο και το 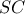 ύψος του . Μετά απ αυτά το
ύψος του . Μετά απ αυτά το  είναι έγκεντρο του
είναι έγκεντρο του  και άρα
και άρα  .
.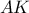 το ύψος του
το ύψος του  . Αν
. Αν  θα είναι :
θα είναι :
 έχω :
έχω : .
.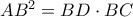 που μας εξασφαλίζει ότι η
που μας εξασφαλίζει ότι η  εφάπτεται του κύκλου
εφάπτεται του κύκλου  οπότε
οπότε  .
.Εστω ότιΜιχάλης Νάννος έγραψε: ↑Πέμ Νοέμ 16, 2017 7:45 amfindx.pngΣτο παραπάνω σχήμα, να βρείτε τη γωνία. Υπάρχουν λύσεις και για "μικρότερο" φάκελο!


Ωραία Γιάννη μου άρεσε !STOPJOHN έγραψε: ↑Πέμ Νοέμ 16, 2017 10:51 amΕστω ότιΜιχάλης Νάννος έγραψε: ↑Πέμ Νοέμ 16, 2017 7:45 amfindx.pngΣτο παραπάνω σχήμα, να βρείτε τη γωνία. Υπάρχουν λύσεις και για "μικρότερο" φάκελο!
Τότε
Γιάννης
Χαιρετώ την παρέα!Μιχάλης Νάννος έγραψε: ↑Πέμ Νοέμ 16, 2017 7:45 amfindx.pngΣτο παραπάνω σχήμα, να βρείτε τη γωνία. Υπάρχουν λύσεις και για "μικρότερο" φάκελο!
 στη
στη  τέμνει την
τέμνει την  στο
στο  κι επειδή
κι επειδή  θα είναι
θα είναι 
 βρίσκω
βρίσκω  και με νόμο συνημιτόνου στο
και με νόμο συνημιτόνου στο 
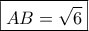


 εύκολα είναι
εύκολα είναι 
 εύκολα είναι
εύκολα είναι