Xαιρετώ ! Ευχαριστώ θερμά τους
Νίκο ,Κώστα και Μιχάλη για τις απαντήσεις !
Να πω για τον
Κώστα ότι είχα την τύχη και την χαρά να τον συναντήσω πριν ένα μήνα στην Λευκάδα !
Ας δώσω για το α' ζητούμενο μια ακόμη προσέγγιση .
Έστω

το
μέσον του

και

η τομή των

. Το

είναι το ένα κοινό σημείο
του κύκλου των

με την

. Αρκεί να δείξουμε ότι το

είναι το άλλο κοινό τους σημείο.
Έχουμε (άσκηση και του σχολικού)

τότε στο ισοσκελές

η
διχοτόμος 
είναι και
ύψος οπότε

ενώ και

(εφαρμογή του σχολικού με

έγκεντρο) επομένως τα

είναι
ομοκυκλικά.

- 4-12-17 Διχοτόμηση...PNG (8.91 KiB) Προβλήθηκε 560 φορές
Στη συνέχεια θα ήθελα να συνδέσω το παρόν με το πρόσφατο σχετικό θέμα του
Θανάση (KARKAR)
ΕΔΩ .
Ο ''ζηλευτός'' λόγος σύγκρισης εμβαδών εκεί (πολύ κοντά στην μονάδα !) άνοιξε τον δρόμο και για τον εδώ λόγο
που βεβαίως είναι ο ίδιος :

. Στην πράξη μετέφερα πάνω το κάτω ημικύκλιο (διάμετροι

)
και αντικατέστησα το μισό τραπέζιο με το τρίγωνο
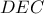
αφού ισχύει

Φιλικά Γιώργος.
 έχει
έχει  και έστω
και έστω  το έγκεντρον αυτού. Το τόξο των
το έγκεντρον αυτού. Το τόξο των  τέμνει την
τέμνει την  στο
στο  .
. διέρχεται από το μέσον
διέρχεται από το μέσον  του ύψους
του ύψους  .
. που τέμνει την
που τέμνει την  στο
στο  .
. 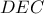 με αυτό του ως άνω ημικυκλίου.
με αυτό του ως άνω ημικυκλίου.
 η τομή του κύκλου
η τομή του κύκλου  με τη
με τη  . Επειδή
. Επειδή 
 ως προς τον κύκλο
ως προς τον κύκλο  .
. . Τώρα από το Θ. Μενελάου στο τρίγωνο
. Τώρα από το Θ. Μενελάου στο τρίγωνο  με διατέμνουσα
με διατέμνουσα  έχω :
έχω : .
. είναι εγγράψιμο και έτσι:
είναι εγγράψιμο και έτσι: 
 .
. = εμβαδόν ημικυκλίου διαμέτρου
= εμβαδόν ημικυκλίου διαμέτρου  .
. εύκολα προκύπτει ότι είναι:
εύκολα προκύπτει ότι είναι:



 έχουμε:
έχουμε: 
 από το νόμο των συνημιτόνων στο τρίγωνο
από το νόμο των συνημιτόνων στο τρίγωνο 

 είναι:
είναι: 

 τότε θα έχουμε:
τότε θα έχουμε:

 μέσο του ύψους
μέσο του ύψους  .
. και
και 
 εγγράψιμο
εγγράψιμο εφαπτόμενη του περίκυκλου του
εφαπτόμενη του περίκυκλου του  .
.
 .Ακόμη,
.Ακόμη,  και
και

 =εμβαδόν του εν λόγω ημικυκλίου
=εμβαδόν του εν λόγω ημικυκλίου
 θα είναι:
θα είναι: 
 προκύπτει:
προκύπτει: 
 υπολογίζουμε:
υπολογίζουμε:



 . Το
. Το  είναι το ένα κοινό σημείο
είναι το ένα κοινό σημείο
 η διχοτόμος
η διχοτόμος  είναι και ύψος οπότε
είναι και ύψος οπότε 
 (εφαρμογή του σχολικού με
(εφαρμογή του σχολικού με  είναι ομοκυκλικά.
είναι ομοκυκλικά.
 . Στην πράξη μετέφερα πάνω το κάτω ημικύκλιο (διάμετροι
. Στην πράξη μετέφερα πάνω το κάτω ημικύκλιο (διάμετροι  )
) 