Σελίδα 1 από 1
Ημικύκλιο εντός κύκλου
Δημοσιεύτηκε: Δευ Μαρ 09, 2020 6:47 pm
από Μιχάλης Νάννος

- shape.png (22.29 KiB) Προβλήθηκε 610 φορές
Δίνεται κύκλος

και δύο χορδές του

. Το ημικύκλιο διαμέτρου

εφάπτεται στην

στο

. Να βρείτε το

, αν
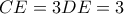
Re: Ημικύκλιο εντός κύκλου
Δημοσιεύτηκε: Δευ Μαρ 09, 2020 7:23 pm
από KARKAR

- tessares.png (25.78 KiB) Προβλήθηκε 596 φορές
... Άρα :

και με Πυθαγόρειο :

Re: Ημικύκλιο εντός κύκλου
Δημοσιεύτηκε: Τρί Μαρ 10, 2020 10:44 am
από george visvikis
Re: Ημικύκλιο εντός κύκλου
Δημοσιεύτηκε: Τρί Μαρ 10, 2020 11:55 am
από Doloros
Re: Ημικύκλιο εντός κύκλου
Δημοσιεύτηκε: Τρί Μαρ 10, 2020 5:57 pm
από Μιχάλης Τσουρακάκης
Μιχάλης Νάννος έγραψε: ↑Δευ Μαρ 09, 2020 6:47 pm
shape.pngΔίνεται κύκλος

και δύο χορδές του

. Το ημικύκλιο διαμέτρου

εφάπτεται στην

στο

. Να βρείτε το

, αν
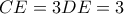
Θεωρώντας και το ημικύκλιο διαμέτρου

η

είναι εφαπτομένη του και

.
Εύκολα με Π.Θ στο

.Το

προφανώς είναι ορθόκεντρο του

και

ρόμβος

και με Π.Θ στο


- Ημικύκλιο εντός κύκλου (2).png (55.86 KiB) Προβλήθηκε 505 φορές
Re: Ημικύκλιο εντός κύκλου
Δημοσιεύτηκε: Τρί Μαρ 10, 2020 7:04 pm
από Doloros
 και δύο χορδές του
και δύο χορδές του  . Το ημικύκλιο διαμέτρου
. Το ημικύκλιο διαμέτρου  εφάπτεται στην
εφάπτεται στην  στο
στο  . Να βρείτε το
. Να βρείτε το  , αν
, αν 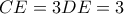
 και δύο χορδές του
και δύο χορδές του  . Το ημικύκλιο διαμέτρου
. Το ημικύκλιο διαμέτρου  εφάπτεται στην
εφάπτεται στην  στο
στο  . Να βρείτε το
. Να βρείτε το  , αν
, αν 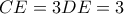
 και με Πυθαγόρειο :
και με Πυθαγόρειο : 








 το σημείο τομής των ίσων χορδών ,
το σημείο τομής των ίσων χορδών ,  . Αφού είναι ίσες θα έχουν ίσα αποστήματα
. Αφού είναι ίσες θα έχουν ίσα αποστήματα  άρα
άρα  .
. έχω:
έχω: 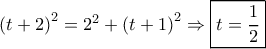
 έχω:
έχω:  . Αφού τώρα
. Αφού τώρα  (
(  το μέσο του
το μέσο του  ) θα είναι :
) θα είναι : 
 βρίσκω:
βρίσκω: 
 και φέρνω το εφαπτόμενο τμήμα
και φέρνω το εφαπτόμενο τμήμα  προς το ημικύκλιο .
προς το ημικύκλιο . και γράφω τον κύκλου
και γράφω τον κύκλου  .
. .
. .Το
.Το  προφανώς είναι ορθόκεντρο του
προφανώς είναι ορθόκεντρο του  και
και  ρόμβος
ρόμβος και με Π.Θ στο
και με Π.Θ στο 
 Άρα
Άρα 
 :
: 