 Το τρίγωνο
Το τρίγωνο  έχει πλευρές
έχει πλευρές  και
και  το έγκεντρο αυτού. Αν
το έγκεντρο αυτού. Αν  με
με  τότε
τότεΝα εξεταστεί αν το
 είναι το βαρύκεντρο του τριγώνου
είναι το βαρύκεντρο του τριγώνου 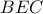 . Σας ευχαριστώ, Γιώργος.
. Σας ευχαριστώ, Γιώργος.Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 Το τρίγωνο
Το τρίγωνο  έχει πλευρές
έχει πλευρές  και
και  το έγκεντρο αυτού. Αν
το έγκεντρο αυτού. Αν  με
με  τότε
τότε είναι το βαρύκεντρο του τριγώνου
είναι το βαρύκεντρο του τριγώνου 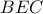 . Σας ευχαριστώ, Γιώργος.
. Σας ευχαριστώ, Γιώργος.Καλημέρα! Στο τρίγωνοΓιώργος Μήτσιος έγραψε: ↑Σάβ Μαρ 28, 2020 7:17 pmΚαλησπέρα. Με αφορμή και την παρατήρηση του Γιώργου εδώ
Εδώ έγκεντρο, εκεί βαρύκεντρο!.PNG
Το τρίγωνο
έχει πλευρές
και
το έγκεντρο αυτού. Αν
με
τότε
Να εξεταστεί αν τοείναι το βαρύκεντρο του τριγώνου
. Σας ευχαριστώ, Γιώργος.
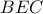 η
η  είναι ύψος και διχοτόμος, οπότε θα είναι και διάμεσος και
είναι ύψος και διχοτόμος, οπότε θα είναι και διάμεσος και 
 βρίσκω
βρίσκω  Αν
Αν  είναι η προβολή του
είναι η προβολή του 
 τότε
τότε  (ως ακτίνα εγγεγραμμένου κύκλου του
(ως ακτίνα εγγεγραμμένου κύκλου του  ). Τα τρίγωνα
). Τα τρίγωνα  είναι ίσα,
είναι ίσα,  δηλαδή
δηλαδή  γεγονός που καθιστά το
γεγονός που καθιστά το  βαρύκεντρο του τριγώνου
βαρύκεντρο του τριγώνου 
 το σημείο τομής των
το σημείο τομής των  με τη
με τη  το
το  θα είναι μέσο της βάσης
θα είναι μέσο της βάσης  του ισοσκελούς τριγώνου
του ισοσκελούς τριγώνου  .
. το σημείο τομής της
το σημείο τομής της  με την
με την  . Θα είναι ( Θ διχοτόμου ),
. Θα είναι ( Θ διχοτόμου ), κι αφού προφανώς
κι αφού προφανώς  θα έχουμε:
θα έχουμε: 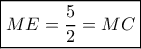 .
. είναι διχοτόμος μεν του
είναι διχοτόμος μεν του  αλλά διάμεσος του
αλλά διάμεσος του  συνεπώς
συνεπώς  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες