 στον κύκλο
στον κύκλο  με πλευρές τις
με πλευρές τις  και με διαγώνιες τις
και με διαγώνιες τις  .
. Αν η διαγώνιος
 είναι η συμμετροδιάμεσος του τριγώνου
είναι η συμμετροδιάμεσος του τριγώνου  κατά τη γωνία
κατά τη γωνία  ,
, τότε να δειχθεί:
1ο)

2o)
 ή
ή 
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 στον κύκλο
στον κύκλο  με πλευρές τις
με πλευρές τις  και με διαγώνιες τις
και με διαγώνιες τις  .
.  είναι η συμμετροδιάμεσος του τριγώνου
είναι η συμμετροδιάμεσος του τριγώνου  κατά τη γωνία
κατά τη γωνία  ,
, 
 ή
ή 
Καλημέρα!
 είναι συμμετροδιάμεσος του
είναι συμμετροδιάμεσος του  1o)
1o)  και ομοίως
και ομοίως  Με διαίρεση κατά μέλη,
Με διαίρεση κατά μέλη, Αλλά,
Αλλά,  (από τα όμοια τρίγωνα
(από τα όμοια τρίγωνα  )
)


 ή
ή 
Γιώργο καλημέρα από Γρεβενά...george visvikis έγραψε: ↑Τρί Ιουν 14, 2022 11:05 amΚαλημέρα!
Σύμφωνα με αυτήν και ηείναι συμμετροδιάμεσος του

1o)και ομοίως
Με διαίρεση κατά μέλη,
Αλλά,
(από τα όμοια τρίγωνα
)
Επομένως,
2o) Από Πτολεμαίο

απ' όπου προκύπτει το ζητούμενοή

 ή
ή 
 η διαγώνιος
η διαγώνιος  είναι συμμετροδιάμεσος του τριγώνου
είναι συμμετροδιάμεσος του τριγώνου  τότε σύμφωνα
τότε σύμφωνα 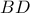 θα είναι συμμετροδιάμεοος του τριγώνου
θα είναι συμμετροδιάμεοος του τριγώνου  και συνεχίζοντας, συμπεραίνουμε ότι η διαγώνιος
και συνεχίζοντας, συμπεραίνουμε ότι η διαγώνιος  θα είναι συμμετροδιάμεσος του τριγώνου
θα είναι συμμετροδιάμεσος του τριγώνου  και τέλος η διαγώνιος
και τέλος η διαγώνιος 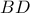 συμμετροδιάμεσος του τριγώνου
συμμετροδιάμεσος του τριγώνου  .
. 




Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες