 τα συμμετρικά του ορθοκέντρου
τα συμμετρικά του ορθοκέντρου  τριγώνου
τριγώνου  ως προς τις ευθείες των πλευρών του
ως προς τις ευθείες των πλευρών του  αντίστοιχα. Να δείξετε ότι η
αντίστοιχα. Να δείξετε ότι η  είναι κάθετη στην ευθεία Euler του τριγώνου
είναι κάθετη στην ευθεία Euler του τριγώνου  , όπου
, όπου  οι ορθές προβολές των
οι ορθές προβολές των  στις
στις 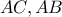 αντίστοιχα.
αντίστοιχα. Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 τα συμμετρικά του ορθοκέντρου
τα συμμετρικά του ορθοκέντρου  τριγώνου
τριγώνου  ως προς τις ευθείες των πλευρών του
ως προς τις ευθείες των πλευρών του  αντίστοιχα. Να δείξετε ότι η
αντίστοιχα. Να δείξετε ότι η  είναι κάθετη στην ευθεία Euler του τριγώνου
είναι κάθετη στην ευθεία Euler του τριγώνου  , όπου
, όπου  οι ορθές προβολές των
οι ορθές προβολές των  στις
στις 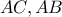 αντίστοιχα.
αντίστοιχα. (Ακόμα μία) εξαιρετική εφαρμογή του Θεωρήματος Στάθη Κούτρα!ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Κυρ Δεκ 04, 2022 8:38 pmΈστωτα συμμετρικά του ορθοκέντρου
τριγώνου
ως προς τις ευθείες των πλευρών του
αντίστοιχα. Να δείξετε ότι η
είναι κάθετη στην ευθεία Euler του τριγώνου
, όπου
οι ορθές προβολές των
στις
αντίστοιχα.
 τα ίχνη των υψών από τα σημεία
τα ίχνη των υψών από τα σημεία  και
και 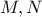 τα μέσα των πλευρών
τα μέσα των πλευρών  , αντίστοιχα. Σύμφωνα λοιπόν με αυτό το Θεώρημα, αρκεί να αποδείξουμε ότι
, αντίστοιχα. Σύμφωνα λοιπόν με αυτό το Θεώρημα, αρκεί να αποδείξουμε ότι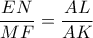


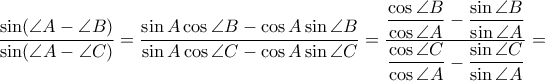

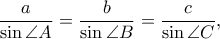
 και
και  , από τον Νόμο Συνημιτόνων δε
, από τον Νόμο Συνημιτόνων δε και ανάλογες εκφράσεις προκύπτουν για τα
και ανάλογες εκφράσεις προκύπτουν για τα  και
και  , οπότε διαιρώντας αυτές κατά μέλη έχουμε τους παραπάνω λόγους.
, οπότε διαιρώντας αυτές κατά μέλη έχουμε τους παραπάνω λόγους.



Να ευχαριστήσω τον Ορέστη για την αντιμετώπιση του προβλήματος και ας δούμε μια διαφορετική προσέγγιση χρησιμοποιώντας όμως το ίδιο θεώρημα Είναι γνωστό ότι τα συμμετρικά του ορθοκέντρου τριγώνου είναι σημεία του περίκυκλου του τριγώνου . ΑνΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Κυρ Δεκ 04, 2022 8:38 pmκαθετοτητα του Darij Grinberg.png
Έστωτα συμμετρικά του ορθοκέντρου
τριγώνου
ως προς τις ευθείες των πλευρών του
αντίστοιχα. Να δείξετε ότι η
είναι κάθετη στην ευθεία Euler του τριγώνου
, όπου
οι ορθές προβολές των
στις
αντίστοιχα.
 είναι λοιπόν το κέντρο του περίκυκλου
είναι λοιπόν το κέντρο του περίκυκλου  του
του  τότε με
τότε με  τις ορθές προβολές του
τις ορθές προβολές του  στις
στις 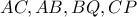 αντίστοιχα , τότε από τα ορθογώνια
αντίστοιχα , τότε από τα ορθογώνια  , όπου
, όπου  τα ίχνη των υψών από τα
τα ίχνη των υψών από τα  αντίστοιχα , προκύπτει ότι οι ορθές προβολές
αντίστοιχα , προκύπτει ότι οι ορθές προβολές  της
της  στις
στις 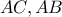 αντίστοιχα , ταυτίζονται (μετρικά) με τα
αντίστοιχα , ταυτίζονται (μετρικά) με τα  αντίστοιχα.
αντίστοιχα. 
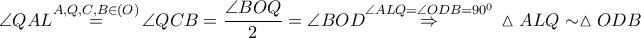
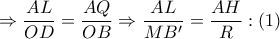


 σύμφωνα με το Stathis Koutras Theorem προκύπτει ότι
σύμφωνα με το Stathis Koutras Theorem προκύπτει ότι  και το ζητούμενο έχει αποδειχθεί .
και το ζητούμενο έχει αποδειχθεί .Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες